【题目】已知椭圆![]() :
: ![]() (
(![]() )的离心率为
)的离心率为![]() ,以椭圆的四个顶点为顶点的四边形的面积为8.
,以椭圆的四个顶点为顶点的四边形的面积为8.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)如图,斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,点
两点,点![]() 在直线
在直线![]() 的左上方.若
的左上方.若![]() ,且直线
,且直线![]() ,
, ![]() 分别与
分别与![]() 轴交于
轴交于![]() ,
, ![]() 点,求线段
点,求线段![]() 的长度.
的长度.

参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析: (1)由已知条件求出![]() 的值,得出椭圆方程; (2)设直线
的值,得出椭圆方程; (2)设直线![]() 的方程, 联立直线与椭圆方程,求出两根之和,两根之积,求出
的方程, 联立直线与椭圆方程,求出两根之和,两根之积,求出![]() ,得到
,得到![]() 为等腰直角三角形,求出线段
为等腰直角三角形,求出线段![]() 的长.
的长.
试题解析:(1)由题意知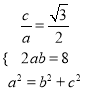 ,解之,得
,解之,得![]() .
.
所以椭圆![]() 的方程为
的方程为![]() ;
;
(2)设直线![]() ,
, ![]() ,
,
将![]() 代入
代入![]() 中,化简整理,得
中,化简整理,得![]() ,
,
![]() ,得
,得![]() ,
,
于是有![]() ,
, ![]() ,
, ![]() ,
,
注意到![]() ,
,
上式中,分子![]()
![]()
![]() ,
,
从而, ![]() ,由
,由![]() ,可知
,可知![]() ,
,
所以![]() 是等腰直角三角形,
是等腰直角三角形, ![]() ,即为所求.
,即为所求.
点睛:本题主要考查了求椭圆方程以及直线与椭圆相交时求另一线段的长,计算量比较大,属于中档题.解题思路:在(1)中,直接由已知条件得出;在(2)中,通过求出![]() ,而
,而![]() ,得出
,得出![]() ,得到
,得到![]() 为等腰直角三角形,再求出线段
为等腰直角三角形,再求出线段![]() 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的多面体中,
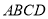 是平行四边形,
是平行四边形, 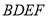 是矩形,
是矩形, 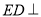 面
面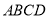 ,
, 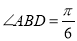 ,
, 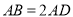 .
.(Ⅰ)求证:平面
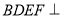 平面
平面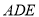 ;
;(Ⅱ)若
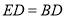 ,求
,求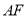 与平面
与平面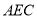 所成角的正弦值.
所成角的正弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
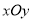 中,直线
中,直线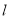 的参数方程为
的参数方程为 (
(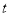 为参数,
为参数, 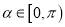 ).以原点
).以原点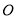 为极点,以
为极点,以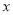 轴正半轴为极轴,与直角坐标系
轴正半轴为极轴,与直角坐标系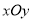 取相同的长度单位,建立极坐标系.设曲线
取相同的长度单位,建立极坐标系.设曲线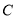 的极坐标方程为
的极坐标方程为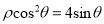 .
.(Ⅰ)设
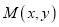 为曲线
为曲线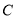 上任意一点,求
上任意一点,求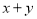 的取值范围;
的取值范围;(Ⅱ)若直线
 与曲线
与曲线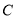 交于两点
交于两点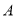 ,
, 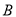 ,求
,求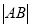 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
质量指标值分组
[75,85)
[85,95)
[95,105)
[105,115)
[115,125)
频数
6
26
38
22
8
(1)作出这些数据的频率分布直方图;
(2)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);

(3)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品80%”的规定?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
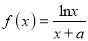 (
(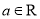 ),曲线
),曲线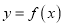 在点
在点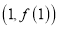 处的切线与直线
处的切线与直线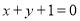 垂直.
垂直.(Ⅰ)试比较
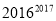 与
与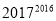 的大小,并说明理由;
的大小,并说明理由;(Ⅱ)若函数
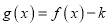 有两个不同的零点
有两个不同的零点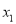 ,
, 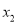 ,证明:
,证明:  .
. -
科目: 来源: 题型:
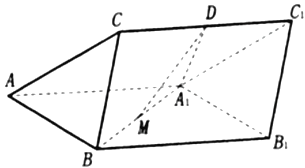
查看答案和解析>>【题目】如图,三棱柱
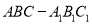 中,
中, 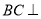 平面
平面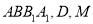 分别为
分别为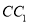 和
和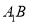 的中点,
的中点, 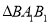 是边长为
是边长为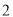 的正三角形,
的正三角形, 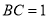 .
.
(1)证明:
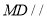 平面
平面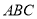 ;
;(2)求二面角
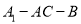 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=x2+bx+c,若f(﹣3)=f(1),f(0)=﹣3.
(1)求函数f(x)的解析式;
(2)若函数g(x)=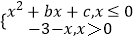 画出函数g(x)图象;
画出函数g(x)图象;
(3)求函数g(x)在[﹣3,1]的最大值和最小值.
相关试题

