【题目】从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
频数 | 6 | 26 | 38 | 22 | 8 |
(1)作出这些数据的频率分布直方图;
(2)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);

(3)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品80%”的规定?
参考答案:
【答案】(1)见解析;(2)平均数的估计值为100,方差的估计值为104;(3)不能认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品80%”的规定.
【解析】试题分析:(1)根据频数算出频率,得纵坐标,即可可做直方图;(2)每组数据中间值乘以该组的频率求和即可得这种产品质量指标值的平均数,再根据方差公式求其方差;(3)不低于![]() 的各组频率求和与
的各组频率求和与![]() 进行比较即可。
进行比较即可。
试题解析:(1)
 。
。
(2)质量指标值的样本平均数为![]()
质量指标值的样本方差为:![]() 。
。
所以这种产品质量指标值的样本平均数的估计值为100,方差的估计值为104。
(3)质量指标值不低于95的产品所占比例的估计值为![]() 。由于该估计值小于0.8,故不能认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品80%”的规定。
。由于该估计值小于0.8,故不能认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品80%”的规定。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某产品的三个质量指标分别为x,y,z,用综合指标S=x+y+z评价该产品的等级.若S≤4, 则该产品为一等品.先从一批该产品中,随机抽取10件产品作为样本,其质量指标列表如下:
产品编号
A1
A2
A3
A4
A5
质量指标
(x, y, z)
(1,1,2)
(2,1,1)
(2,2,2)
(1,1,1)
(1,2,1)
产品编号
A6
A7
A8
A9
A10
质量指标
(x, y, z)
(1,2,2)
(2,1,1)
(2,2,1)
(1,1,1)
(2,1,2)
(1)利用上表提供的样本数据估计该批产品的一等品率;
(2)在该样本的一等品中, 随机抽取2件产品,
(ⅰ) 用产品编号列出所有可能的结果;
(ⅱ) 设事件B为“在取出的2件产品中, 每件产品的综合指标S都等于4”, 求事件B发生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的多面体中,
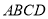 是平行四边形,
是平行四边形, 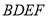 是矩形,
是矩形, 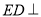 面
面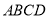 ,
, 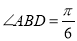 ,
, 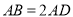 .
.(Ⅰ)求证:平面
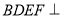 平面
平面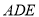 ;
;(Ⅱ)若
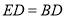 ,求
,求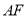 与平面
与平面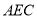 所成角的正弦值.
所成角的正弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
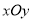 中,直线
中,直线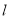 的参数方程为
的参数方程为 (
(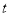 为参数,
为参数, 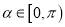 ).以原点
).以原点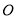 为极点,以
为极点,以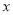 轴正半轴为极轴,与直角坐标系
轴正半轴为极轴,与直角坐标系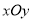 取相同的长度单位,建立极坐标系.设曲线
取相同的长度单位,建立极坐标系.设曲线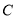 的极坐标方程为
的极坐标方程为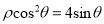 .
.(Ⅰ)设
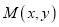 为曲线
为曲线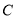 上任意一点,求
上任意一点,求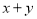 的取值范围;
的取值范围;(Ⅱ)若直线
 与曲线
与曲线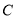 交于两点
交于两点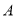 ,
, 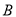 ,求
,求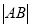 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
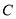 :
: 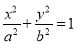 (
(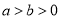 )的离心率为
)的离心率为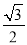 ,以椭圆的四个顶点为顶点的四边形的面积为8.
,以椭圆的四个顶点为顶点的四边形的面积为8.(Ⅰ)求椭圆
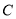 的方程;
的方程;(Ⅱ)如图,斜率为
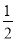 的直线
的直线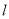 与椭圆
与椭圆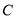 交于
交于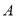 ,
, 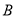 两点,点
两点,点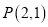 在直线
在直线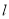 的左上方.若
的左上方.若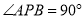 ,且直线
,且直线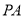 ,
,  分别与
分别与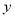 轴交于
轴交于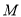 ,
, 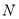 点,求线段
点,求线段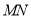 的长度.
的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
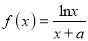 (
(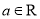 ),曲线
),曲线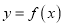 在点
在点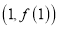 处的切线与直线
处的切线与直线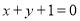 垂直.
垂直.(Ⅰ)试比较
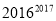 与
与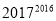 的大小,并说明理由;
的大小,并说明理由;(Ⅱ)若函数
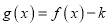 有两个不同的零点
有两个不同的零点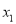 ,
, 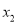 ,证明:
,证明:  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱
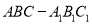 中,
中, 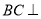 平面
平面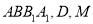 分别为
分别为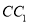 和
和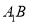 的中点,
的中点, 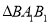 是边长为
是边长为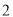 的正三角形,
的正三角形, 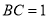 .
.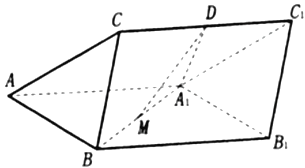
(1)证明:
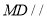 平面
平面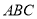 ;
;(2)求二面角
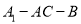 的余弦值.
的余弦值.
相关试题

