【题目】如图所示,一根水平放置的长方体枕木的安全负荷与它的厚度d的平方和宽度a的乘积成正比,与它的长度l的平方成反比. 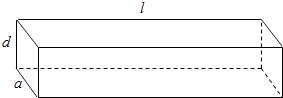
(1)在a>d>0的条件下,将此枕木翻转90°(即宽度变为了厚度),枕木的安全负荷会发生变化吗?变大还是变小?
(2)现有一根横截面为半圆(半圆的半径为R= ![]() )的柱形木材,用它截取成横截面为长方形的枕木,其长度即为枕木规定的长度l,问横截面如何截取,可使安全负荷最大?
)的柱形木材,用它截取成横截面为长方形的枕木,其长度即为枕木规定的长度l,问横截面如何截取,可使安全负荷最大?
参考答案:
【答案】
(1)解:设安全负荷为 ![]()
翻转90°后 ![]() ,
,
可得: ![]() ,
,
当a>d>0时, ![]() <1
<1
此时枕木的安全负荷变大.
(2)解:设截取的宽为a(0<a<2 ![]() ),高为d,
),高为d, ![]() ,∴a2+d2=12
,∴a2+d2=12
其长度l及k为定值,安全负荷为 ![]()
令 ![]() ,
, ![]()
此时 ![]()
由g′(a)<0,可得 ![]() ,
,
∴ ![]()
所以当宽a=2时,g(a)取得取大值,此时高 ![]() ,
,
所以,当宽a=2,高 ![]() 时,安全负荷最大
时,安全负荷最大
【解析】(1)设安全负荷为 ![]() ,求出翻转90°后的表达式,然后求解比值的最大值.(2)设截取的宽为a(0<a<2
,求出翻转90°后的表达式,然后求解比值的最大值.(2)设截取的宽为a(0<a<2 ![]() ),高为d,
),高为d, ![]() ,得到安全负荷为
,得到安全负荷为 ![]()
令 ![]() ,
, ![]() 利用函数的导数求解最大值即可.
利用函数的导数求解最大值即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种产品的广告费支出x与销售额y(单位:万元)之间有如表对应数据:
x
2
4
5
6
8
y
30
40
60
50
70
(1)求广告费支出x与销售额y回归直线方程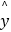 =bx+a(a,b∈R);
=bx+a(a,b∈R);
已知b=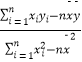 ,
, 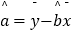
(2)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值不超过5的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】来自某校一班和二班的共计9名学生志愿服务者被随机平均分配到运送矿泉水、清扫卫生、维持秩序这三个岗位服务,且运送矿泉水岗位至少有一名一班志愿者的概率是
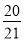 .
.(Ⅰ)求清扫卫生岗位恰好一班1人、二班2人的概率;
(Ⅱ)设随机变量
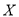 为在维持秩序岗位服务的一班的志愿者的人数,求
为在维持秩序岗位服务的一班的志愿者的人数,求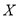 分布列及期望.
分布列及期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】若f(x)是定义在R上的增函数,下列函数中
①y=[f(x)]2是增函数;
②y=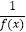 是减函数;
是减函数;
③y=﹣f(x)是减函数;
④y=|f(x)|是增函数;
其中正确的结论是( )
A.③
B.②③
C.②④
D.①③ -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 :
:  经过点
经过点 ,左右焦点分别为
,左右焦点分别为 、
、 ,圆
,圆 与直线
与直线 相交所得弦长为2.
相交所得弦长为2. (Ⅰ)求椭圆
 的标准方程;
的标准方程;(Ⅱ)设
 是椭圆
是椭圆 上不在
上不在 轴上的一个动点,
轴上的一个动点,  为坐标原点,过点
为坐标原点,过点 作
作 的平行线交椭圆
的平行线交椭圆 于
于 、
、 两个不同的点.
两个不同的点.(1)试探究
 的值是否为一个常数?若是,求出这个常数;若不是,请说明理由.
的值是否为一个常数?若是,求出这个常数;若不是,请说明理由.(2)记
 的面积为
的面积为 ,
,  的面积为
的面积为 ,令
,令 ,求
,求 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
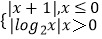 ,若方程f(x)=a有四个不同的解x1 , x2 , x3 , x4 , 且x1<x2<x3<x4 , 则x3(x1+x2)+
,若方程f(x)=a有四个不同的解x1 , x2 , x3 , x4 , 且x1<x2<x3<x4 , 则x3(x1+x2)+ 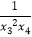 的取值范围是( )
的取值范围是( )
A.(﹣1,+∞)
B.(﹣1,1]
C.(﹣∞,1)
D.[﹣1,1) -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司的两个部门招聘工作人员,应聘者从 T1、T2两组试题中选择一组参加测试,成绩合格者可签约.甲、乙、丙、丁四人参加应聘考试,其中甲、乙两人选择使用试题 T1 , 且表示只要成绩合格就签约;丙、丁两人选择使用试题 T2 , 并约定:两人成绩都合格就一同签约,否则两人都不签约.已知甲、乙考试合格的概率都是
 ,丙、丁考试合格的概率都是
,丙、丁考试合格的概率都是  ,且考试是否合格互不影响.
,且考试是否合格互不影响.
(1)求丙、丁未签约的概率;
(2)记签约人数为 X,求 X的分布列和数学期望EX.
相关试题

