搜索
【题目】已知函数f（x）= 
，若方程f（x）=a有四个不同的解x1 ， x2 ， x3 ， x4 ， 且x1＜x2＜x3＜x4 ， 则x3（x1+x2）+ 
的取值范围是（ ）
A.（﹣1，+∞）
B.（﹣1，1]
C.（﹣∞，1）
D.[﹣1，1）
参考答案：
【答案】B
【解析】解：作函数f（x）= 
，的图象如下，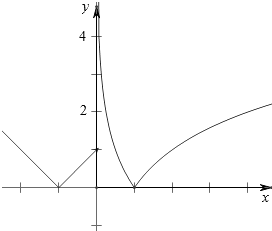 
由图可知，x1+x2=﹣2，x3x4=1；1＜x4≤2；
故x3（x1+x2）+ 
=﹣ 
+x4 ，
其在1＜x4≤2上是增函数，
故﹣2+1＜﹣ +x4≤﹣1+2；
即﹣1＜﹣ +x4≤1；
故选B．
作函数f（x）= 的图象如下，由图象可得x1+x2=﹣2，x3x4=1；1＜x4≤2；从而化简x3（x1+x2）+ ，利用函数的单调性求取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】若f（x）是定义在R上的增函数，下列函数中
①y=[f（x）]2是增函数；
②y=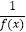
是减函数；
③y=﹣f（x）是减函数；
④y=|f（x）|是增函数；
其中正确的结论是（ ）
A.③
B.②③
C.②④
D.①③ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，一根水平放置的长方体枕木的安全负荷与它的厚度d的平方和宽度a的乘积成正比，与它的长度l的平方成反比．
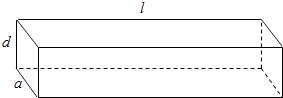
（1）在a＞d＞0的条件下，将此枕木翻转90°（即宽度变为了厚度），枕木的安全负荷会发生变化吗？变大还是变小？
（2）现有一根横截面为半圆（半圆的半径为R=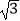
）的柱形木材，用它截取成横截面为长方形的枕木，其长度即为枕木规定的长度l，问横截面如何截取，可使安全负荷最大？ -
科目： 来源： 题型：
查看答案和解析>>【题目】已知椭圆
： 
经过点
，左右焦点分别为
、
，圆
与直线
相交所得弦长为2． （Ⅰ）求椭圆
的标准方程；（Ⅱ）设
是椭圆
上不在
轴上的一个动点， 
为坐标原点，过点
作
的平行线交椭圆
于
、
两个不同的点．（1）试探究
的值是否为一个常数？若是，求出这个常数；若不是，请说明理由．（2）记
的面积为
， 
的面积为
，令
，求
的最大值． -
科目： 来源： 题型：
查看答案和解析>>【题目】某公司的两个部门招聘工作人员，应聘者从 T1、T2两组试题中选择一组参加测试，成绩合格者可签约．甲、乙、丙、丁四人参加应聘考试，其中甲、乙两人选择使用试题 T1 ， 且表示只要成绩合格就签约；丙、丁两人选择使用试题 T2 ， 并约定：两人成绩都合格就一同签约，否则两人都不签约．已知甲、乙考试合格的概率都是
，丙、丁考试合格的概率都是 
，且考试是否合格互不影响．
（1）求丙、丁未签约的概率；
（2）记签约人数为 X，求 X的分布列和数学期望EX． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示的多面体是由一个直平行六面体被平面
所截后得到的，其中
， 
， 
．
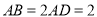（Ⅰ）求证：
平面
；（Ⅱ）求直线
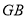与平面
所成角的正弦值． -
科目： 来源： 题型：
查看答案和解析>>【题目】设函数f（x）=x2+bx﹣alnx．
（1）若x=2是函数f（x）的极值点，1和x0是函数f（x）的两个不同零点，且x0∈（n，n+1），n∈N，求n．
（2）若对任意b∈[﹣2，﹣1]，都存在x∈（1，e）（e为自然对数的底数），使得f（x）＜0成立，求实数a的取值范围．
相关试题
