【题目】在平面直角坐标系中,长度为3的线段![]() 的端点
的端点![]() 、
、![]() 分别在
分别在![]() ,
,![]() 轴上滑动,点
轴上滑动,点![]() 在线段
在线段![]() 上,且
上,且![]() ,
,
(1)若点![]() 的轨迹为曲线
的轨迹为曲线![]() ,求其方程;
,求其方程;
(2)过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于不同两点
交于不同两点![]() 、
、![]() ,
,![]() 是曲线上不同于
是曲线上不同于![]() 、
、![]() 的动点,求
的动点,求![]() 面积的最大值.
面积的最大值.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)求轨迹问题可用相关点法得到轨迹方程;
(2)设出直线方程,直曲联立,得到一元二次方程,通过韦达定理表示出面积函数,从而求导求最值即可得到答案.
解:(1)由题知![]() ,设
,设![]() ,
,![]() ,
,![]()
有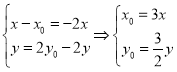 代入
代入![]() 得
得![]() ,
,
所以曲线![]() 的方程是
的方程是![]()
(2)当直线的斜率不存在时,即![]() :
:![]() ,此时
,此时![]()
当直线的斜率存在时,设![]() :
:![]() ,
,![]() ,
,![]() ,
,
联立![]() ,有
,有![]() ,
,![]()
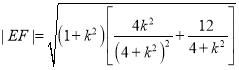
由题知过![]() 的直线
的直线![]() ,且
,且![]() 与椭圆切于
与椭圆切于![]() 点时,
点时,![]() 最大,故设
最大,故设![]() :
:![]()
联立![]() 与椭圆方程得
与椭圆方程得![]() ,此时
,此时![]()
![]() 与
与![]() 的距离
的距离![]() ,所以
,所以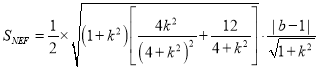
化简![]()
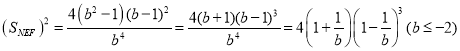
设![]() ,
,![]() ,有
,有![]()
![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递减,当
上单调递减,当![]() 时,函数
时,函数![]() 取得最大值
取得最大值![]() ,即
,即![]() 时
时![]() ,
,
综上所述![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两支篮球队赛季总决赛采用7场4胜制,每场必须分出胜负,场与场之间互不影响,只要有一队获胜4场就结束比赛.现已比赛了4场,且甲篮球队胜3场.已知甲球队第5,6场获胜的概率均为
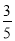 ,但由于体力原因,第7场获胜的概率为
,但由于体力原因,第7场获胜的概率为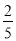 .
.(1)求甲队分别以
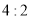 ,
,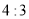 获胜的概率;
获胜的概率;(2)设
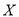 表示决出冠军时比赛的场数,求
表示决出冠军时比赛的场数,求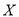 的分布列及数学期望.
的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知参加某项活动的六名成员排成一排合影留念,且甲乙两人均在丙领导人的同侧,则不同的排法共有( )
A. 240种 B. 360种 C. 480种 D. 600种
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 为椭圆
为椭圆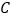 的左、右顶点,
的左、右顶点,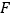 为其右焦点,
为其右焦点,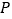 是椭圆
是椭圆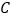 上异于
上异于 的动点,且
的动点,且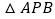 面积的最大值为
面积的最大值为 .
.(1)求椭圆
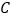 的方程;
的方程;(2)直线
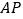 与椭圆在点
与椭圆在点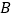 处的切线交于点
处的切线交于点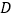 ,当点
,当点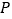 在椭圆上运动时,求证:以
在椭圆上运动时,求证:以  为直径的圆与直线
为直径的圆与直线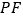 恒相切.
恒相切. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知半径为
 的圆的圆心在
的圆的圆心在 轴上,圆心的横坐标是整数,且与直线
轴上,圆心的横坐标是整数,且与直线 相切.
相切.(Ⅰ)求圆的方程;
(Ⅱ)设直线

 与圆相交于
与圆相交于 两点,求实数
两点,求实数 的取值范围;
的取值范围;(Ⅲ) 在(Ⅱ)的条件下,是否存在实数
 ,使得弦
,使得弦 的垂直平分线
的垂直平分线 过点
过点 ,若存在,求出实数
,若存在,求出实数 的值;若不存在,请说明理由
的值;若不存在,请说明理由 -
科目: 来源: 题型:
查看答案和解析>>【题目】中国古代儒家要求学生掌握六种基本才艺:礼、乐、射、御、书、数,简称“六艺”,某高中学校为弘扬“六艺”的传统文化,分别进行了主题为“礼、乐、射、御、书、数”六场传统文化知识竞赛,现有甲、乙、丙三位选手进入了前三名的最后角逐,规定:每场知识竞赛前三名的得分都分别为
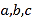
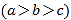 且
且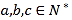 ;选手最后得分为各场得分之和,在六场比赛后,已知甲最后得分为
;选手最后得分为各场得分之和,在六场比赛后,已知甲最后得分为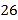 分,乙和丙最后得分都是
分,乙和丙最后得分都是 分,且乙在其中一场比赛中获得第一名,下列说法正确的是( )
分,且乙在其中一场比赛中获得第一名,下列说法正确的是( )A. 乙有四场比赛获得第三名
B. 每场比赛第一名得分
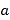 为
为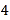
C. 甲可能有一场比赛获得第二名
D. 丙可能有一场比赛获得第一名
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知双曲线
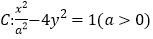 的右顶点到其一条渐近线的距离等于
的右顶点到其一条渐近线的距离等于 ,抛物线
,抛物线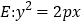 的焦点与双曲线
的焦点与双曲线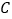 的右焦点重合,则抛物线
的右焦点重合,则抛物线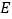 上的动点
上的动点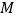 到直线
到直线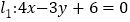 和
和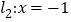 距离之和的最小值为( )
距离之和的最小值为( )A. 1 B. 2 C. 3 D. 4
相关试题

