搜索
【题目】设直线l的方程为（a+1）x+y+2﹣a=0（a∈R）．
（1）若l在两坐标轴上的截距相等，求l的方程；
（2）若l不经过第二象限，求实数a的取值范围．
参考答案：
【答案】
（1）解：令x=0，得y=a﹣2． 令y=0，得 
（a≠﹣1）．
∵l在两坐标轴上的截距相等，∴ 
，解之，得a=2或a=0．
∴所求的直线l方程为3x+y=0或x+y+2=0
（2）解：直线l的方程可化为 y=﹣（a+1）x+a﹣2．∵l不过第二象限，
∴ 
，∴a≤﹣1．∴a的取值范围为（﹣∞，﹣1]
【解析】（1）先求出直线l在两坐标轴上的截距，再利用 l在两坐标轴上的截距相等 建立方程，解方程求出a的值，从而得到所求的直线l方程．（2）把直线l的方程可化为 y=﹣（a+1）x+a﹣2，由题意得 ，解不等式组求得a的范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】设△ABC的内角A，B，C所对的边分别为a，b，c，已知a=2，b=3，cosC=
．
（1）求△ABC的面积；
（2）求sin（C﹣A）的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】两条平行直线和圆的位置关系定义为：若两条平行直线和圆有四个不同的公共点，则称两条平行线和圆“相交”；若两平行直线和圆没有公共点，则称两条平行线和圆“相离”；若两平行直线和圆有一个、两个或三个不同的公共点，则称两条平行线和圆“相切”．已知直线l1：2x﹣y+a=0，l2：2x﹣y+a2+1=0和圆：x2+y2+2x﹣4=0相切，则a的取值范围是（ ）
A.a＞7或a＜﹣3
B.
C.﹣3≤a≤一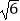
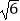或 ≤a≤7
D.a≥7或a≤﹣3 -
科目： 来源： 题型：
查看答案和解析>>【题目】已知中心在原点的双曲线C的右焦点为（2，0），右顶点为（
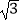，0）
（1）求双曲线C的方程；
（2）若直线l：y=kx+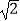
与双曲线C恒有两个不同的交点A和B，且 
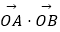＞2（其中O为原点）．求k的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系
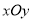中，曲线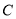
的参数方程为
(
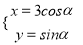为参数），在以原点为极点，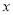 
轴正半轴为极轴的极坐标系中，直线
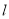的极坐标方程为
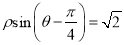.（1）求
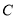的普通方程和
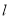的倾斜角；（2）设点
和
交于
两点，求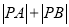
. -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，椭圆E：
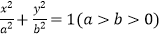的左焦点为F1 ， 右焦点为F2 ， 离心率e= 
．过F1的直线交椭圆于A、B两点，且△ABF2的周长为8．
（Ⅰ）求椭圆E的方程．
（Ⅱ）设动直线l：y=kx+m与椭圆E有且只有一个公共点P，且与直线x=4相交于点Q．试探究：在坐标平面内是否存在定点M，使得以PQ为直径的圆恒过点M？若存在，求出点M的坐标；若不存在，说明理由．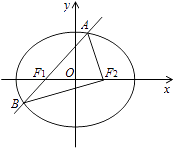
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图为一简单组合体，其底面 ABCD为正方形，PD⊥平面ABCD，EC∥PD，且PD=AD=2EC=2．
（1）求证：BE∥平面PDA；
（2）求四棱锥B﹣CEPD的体积．
相关试题
