【题目】如图,椭圆E: ![]() 的左焦点为F1 , 右焦点为F2 , 离心率e=
的左焦点为F1 , 右焦点为F2 , 离心率e= ![]() .过F1的直线交椭圆于A、B两点,且△ABF2的周长为8.
.过F1的直线交椭圆于A、B两点,且△ABF2的周长为8.
(Ⅰ)求椭圆E的方程.
(Ⅱ)设动直线l:y=kx+m与椭圆E有且只有一个公共点P,且与直线x=4相交于点Q.试探究:在坐标平面内是否存在定点M,使得以PQ为直径的圆恒过点M?若存在,求出点M的坐标;若不存在,说明理由.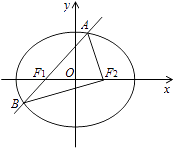
参考答案:
【答案】解:(Ⅰ)∵过F1的直线交椭圆于A、B两点,且△ABF2的周长为8.
∴4a=8,∴a=2
∵e= ![]() ,∴c=1
,∴c=1
∴b2=a2﹣c2=3
∴椭圆E的方程为 ![]() .
.
(Ⅱ)由 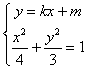 ,消元可得(4k2+3)x2+8kmx+4m2﹣12=0
,消元可得(4k2+3)x2+8kmx+4m2﹣12=0
∵动直线l:y=kx+m与椭圆E有且只有一个公共点P(x0 , y0)
∴m≠0,△=0,∴(8km)2﹣4×(4k2+3)×(4m2﹣12)=0
∴4k2﹣m2+3=0①
此时x0= ![]() =
= ![]() ,y0=
,y0= ![]() ,即P(
,即P( ![]() ,
, ![]() )
)
由 ![]() 得Q(4,4k+m)
得Q(4,4k+m)
取k=0,m= ![]() ,此时P(0,
,此时P(0, ![]() ),Q(4,
),Q(4, ![]() ),以PQ为直径的圆为(x﹣2)2+(y﹣
),以PQ为直径的圆为(x﹣2)2+(y﹣ ![]() )2=4,交x轴于点M1(1,0)或M2(3,0)
)2=4,交x轴于点M1(1,0)或M2(3,0)
取k= ![]() ,m=2,此时P(1,
,m=2,此时P(1, ![]() ),Q(4,0),以PQ为直径的圆为(x﹣
),Q(4,0),以PQ为直径的圆为(x﹣ ![]() )2+(y﹣
)2+(y﹣ ![]() )2=
)2= ![]() ,交x轴于点M3(1,0)或M4(4,0)
,交x轴于点M3(1,0)或M4(4,0)
故若满足条件的点M存在,只能是M(1,0),证明如下
∵ ![]()
∴ ![]()
故以PQ为直径的圆恒过x轴上的定点M(1,0)
方法二:
假设平面内存在定点M满足条件,因为对于任意以PQ为直径的圆恒过定点M,所以当PQ平行于x轴时,圆也过定点M,即此时P点坐标为(0, ![]() )或(0,﹣
)或(0,﹣ ![]() ),由图形对称性知两个圆在x轴上过相同的交点,即点M必在x轴上.设M(x1 , 0),则
),由图形对称性知两个圆在x轴上过相同的交点,即点M必在x轴上.设M(x1 , 0),则 ![]() =0对满足①式的m,k恒成立.
=0对满足①式的m,k恒成立.
因为 ![]() =(﹣
=(﹣ ![]() ﹣x1 ,
﹣x1 , ![]() ),
),![]() =(4﹣x1 , 4k+m),由
=(4﹣x1 , 4k+m),由 ![]() =0得﹣
=0得﹣ ![]() +
+ ![]() ﹣4x1+x12+
﹣4x1+x12+ ![]() +3=0,
+3=0,
整理得(4x1﹣4) ![]() +x12﹣4x1+3=0.②
+x12﹣4x1+3=0.②
由于②式对满足①式的m,k恒成立,所以 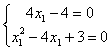 ,解得x1=1.
,解得x1=1.
故存在定点M(1,0),使得以PQ为直径的圆恒过点M
【解析】(Ⅰ)根据过F1的直线交椭圆于A、B两点,且△ABF2的周长为8,可得4a=8,即a=2,利用e= ![]() ,b2=a2﹣c2=3,即可求得椭圆E的方程.(Ⅱ)由
,b2=a2﹣c2=3,即可求得椭圆E的方程.(Ⅱ)由 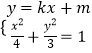 ,消元可得(4k2+3)x2+8kmx+4m2﹣12=0,利用动直线l:y=kx+m与椭圆E有且只有一个公共点P(x0 , y0),可得m≠0,△=0,进而可得P(
,消元可得(4k2+3)x2+8kmx+4m2﹣12=0,利用动直线l:y=kx+m与椭圆E有且只有一个公共点P(x0 , y0),可得m≠0,△=0,进而可得P( ![]() ,
, ![]() ),由
),由 ![]() 得Q(4,4k+m),取k=0,m=
得Q(4,4k+m),取k=0,m= ![]() ;k=
;k= ![]() ,m=2,猜想满足条件的点M存在,只能是M(1,0),再进行证明即可.
,m=2,猜想满足条件的点M存在,只能是M(1,0),再进行证明即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知中心在原点的双曲线C的右焦点为(2,0),右顶点为(
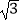 ,0)
,0)
(1)求双曲线C的方程;
(2)若直线l:y=kx+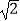 与双曲线C恒有两个不同的交点A和B,且
与双曲线C恒有两个不同的交点A和B,且 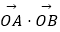 >2(其中O为原点).求k的取值范围.
>2(其中O为原点).求k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设直线l的方程为(a+1)x+y+2﹣a=0(a∈R).
(1)若l在两坐标轴上的截距相等,求l的方程;
(2)若l不经过第二象限,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
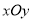 中,曲线
中,曲线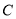 的参数方程为
的参数方程为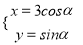 (
( 为参数),在以原点为极点,
为参数),在以原点为极点, 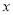 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线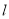 的极坐标方程为
的极坐标方程为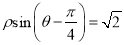 .
.(1)求
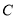 的普通方程和
的普通方程和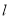 的倾斜角;
的倾斜角;(2)设点
 和
和 交于
交于 两点,求
两点,求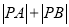 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图为一简单组合体,其底面 ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2.

(1)求证:BE∥平面PDA;
(2)求四棱锥B﹣CEPD的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
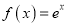 ,直线
,直线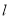 的方程为
的方程为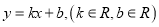 .
.(1)若直线
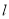 是曲线
是曲线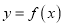 的切线,求证:
的切线,求证: 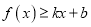 对任意
对任意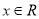 成立;
成立;(2)若
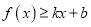 对任意
对任意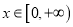 恒成立,求实数是
恒成立,求实数是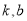 应满足的条件.
应满足的条件. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
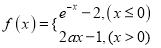 (
(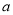 是常数且
是常数且 ),对于下列命题:
),对于下列命题:①函数
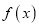 的最小值是
的最小值是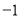 ;
;②函数
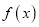 在
在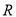 上是单调函数;
上是单调函数;③若
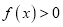 在
在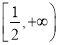 上恒成立,则
上恒成立,则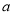 的取值范围是
的取值范围是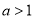 ;
;④对任意的
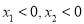 且
且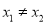 ,恒有
,恒有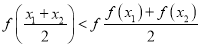
其中正确命题的序号是__________.
相关试题

