【题目】设f(x)是定义在R 且周期为1的函数,在区间![]() 上,
上, ![]() 其中集合D=
其中集合D=![]() ,则方程f(x)-lgx=0的解的个数是____________
,则方程f(x)-lgx=0的解的个数是____________
参考答案:
【答案】8
【解析】由于![]() ,则需考虑
,则需考虑![]() 的情况,
的情况,
在此范围内, ![]() 且
且![]() 时,设
时,设![]() ,且
,且![]() 互质,
互质,
若![]() ,则由
,则由![]() ,可设
,可设![]() ,且
,且![]() 互质,
互质,
因此![]() ,则
,则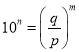 ,此时左边为整数,右边为非整数,矛盾,因此
,此时左边为整数,右边为非整数,矛盾,因此![]() ,
,
因此![]() 不可能与每个周期内
不可能与每个周期内![]() 对应的部分相等,
对应的部分相等,
只需考虑![]() 与每个周期
与每个周期![]() 的部分的交点,
的部分的交点,
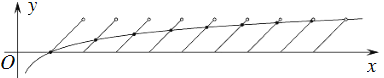
画出函数图象,图中交点除外![]() 其他交点横坐标均为无理数,属于每个周期
其他交点横坐标均为无理数,属于每个周期![]() 的部分,
的部分,
且![]() 处
处![]() ,则在
,则在![]() 附近仅有一个交点,
附近仅有一个交点,
因此方程![]() 的解的个数为8.
的解的个数为8.
点睛:对于方程解的个数(或函数零点个数)问题,可利用函数的值域或最值,结合函数的单调性、草图确定其中参数范围.从图象的最高点、最低点,分析函数的最值、极值;从图象的对称性,分析函数的奇偶性;从图象的走向趋势,分析函数的单调性、周期性等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
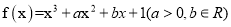 有极值,且导函数
有极值,且导函数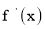 的极值点是
的极值点是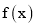 的零点。(极值点是指函数取极值时对应的自变量的值)
的零点。(极值点是指函数取极值时对应的自变量的值)求b关于a的函数关系式,并写出定义域;
证明:b>3a;
若
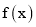 ,
, 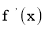 这两个函数的所有极值之和不小于
这两个函数的所有极值之和不小于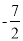 ,求a的取值范围。
,求a的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,平面四边形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AD⊥ED,AF∥DE,AB∥CD,CD=2AB=2AD=2ED=xAF.
(Ⅰ)若四点F、B、C、E共面,AB=a,求x的值;
(Ⅱ)求证:平面CBE⊥平面EDB;
(Ⅲ)当x=2时,求二面角F﹣EB﹣C的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在四棱锥P﹣ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,PA=
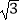 ,AB=1.AD=2.∠BAD=120°,E,F,G,H分别是BC,PB,PC,AD的中点.
,AB=1.AD=2.∠BAD=120°,E,F,G,H分别是BC,PB,PC,AD的中点.
(Ⅰ)求证:PH∥平面GED;
(Ⅱ)过点F作平面α,使ED∥平面α,当平面α⊥平面EDG时,设PA与平面α交于点Q,求PQ的长.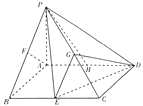
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于给定的正整数k,若数列{an}满足
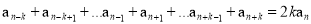
=2kan对任意正整数n(n> k) 总成立,则称数列{an} 是“P(k)数列”.
(1)证明:等差数列{an}是“P(3)数列”;
若数列{an}既是“P(2)数列”,又是“P(3)数列”,证明:{an}是等差数列.
-
科目: 来源: 题型:
查看答案和解析>>【题目】[选修4-4:坐标系与参数方程]在平面坐标系中xOy中,已知直线l的参考方程为
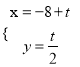 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为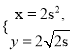 (s为参数)。设p为曲线C上的动点,求点P到直线l的距离的最小值
(s为参数)。设p为曲线C上的动点,求点P到直线l的距离的最小值 -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系中,已知曲线
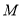 的参数方程为
的参数方程为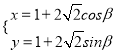 (
(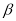 为参数),在极坐标系中,直线
为参数),在极坐标系中,直线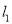 的方程为:
的方程为: 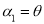 ,直线
,直线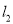 的方程为
的方程为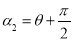 .
.(Ⅰ)写出曲线
 的直角坐标方程,并指出它是何种曲线;
的直角坐标方程,并指出它是何种曲线;(Ⅱ)设
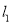 与曲线
与曲线 交于
交于 两点,
两点, 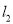 与曲线
与曲线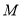 交于
交于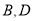 两点,求四边形
两点,求四边形 面积的取值范围.
面积的取值范围.
相关试题

