【题目】数列{an}的前n项和记为Sn , a1=2,an+1=Sn+2(n∈N*).
(Ⅰ)求{an}的通项公式;
(Ⅱ)求数列{nan}的前n项和Tn .
参考答案:
【答案】解:(Ⅰ)由a1=2,an+1=Sn+2(n∈N*),①
an=Sn﹣1+2(n≥2),②…(2分)
①﹣②,得 ![]() (n≥2).
(n≥2).
又由a2=S1+2=4,得 ![]() .
.
所以 ![]() (n≥1),数列{an}是以2为首项,2为公比的等比数列,故
(n≥1),数列{an}是以2为首项,2为公比的等比数列,故 ![]() .
.
(Ⅱ)由(Ⅰ),得 ![]() ,③
,③
2Tn=1×22+2×33+3×24+…+n×2n+1,④
③﹣④,得 ![]() .
.
所以 ![]()
【解析】(Ⅰ)由已知利用递推公式可得到![]() 等于2,进而得证数列{an}是等比数列即可求出通项公式。(Ⅱ)整理数列{nan}的前n项和Tn,两边乘以公比与原式相减即得 Tn。
等于2,进而得证数列{an}是等比数列即可求出通项公式。(Ⅱ)整理数列{nan}的前n项和Tn,两边乘以公比与原式相减即得 Tn。
【考点精析】根据题目的已知条件,利用数列的前n项和和数列的通项公式的相关知识可以得到问题的答案,需要掌握数列{an}的前n项和sn与通项an的关系 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图动直线l:y=b与抛物线y2=4x交于点A,与椭圆
 =1交于抛物线右侧的点B,F为抛物线的焦点,则|AF|+|BF|+|AB|的最大值为( )
=1交于抛物线右侧的点B,F为抛物线的焦点,则|AF|+|BF|+|AB|的最大值为( )
A.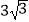
B.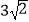
C.2
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=ex(sinx﹣cosx)(0≤x≤2016π),则函数f(x)的各极大值之和为( )
A.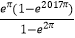
B.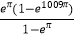
C.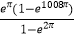
D.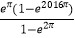
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c分别为△ABC三个内角A,B,C的对边,ccosA+
 csinA﹣b﹣a=0.
csinA﹣b﹣a=0.
(Ⅰ)求C;
(Ⅱ)若c=1,求△ABC的面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
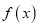 对任意实数
对任意实数 均有
均有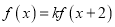 ,其中常数
,其中常数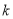 为负数,且
为负数,且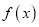 在区间
在区间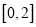 上有表达式
上有表达式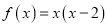 .
.(1)写出
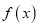 在
在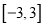 上的表达式,并写出函数
上的表达式,并写出函数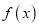 在
在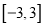 上的单调区间(不用过程,直接写出即可);
上的单调区间(不用过程,直接写出即可);(2)求出
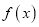 在
在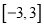 上的最小值与最大值,并求出相应的自变量的取值.
上的最小值与最大值,并求出相应的自变量的取值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,
,  ,函数
,函数 .
.(1)求
 在区间
在区间 上的最大值和最小值;
上的最大值和最小值;(2)若
 ,
,  ,求
,求 的值;
的值;(3)若函数
 在区间
在区间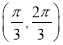 上是单调递增函数,求正数
上是单调递增函数,求正数 的取值范围.
的取值范围.
相关试题

