【题目】设函数f(x)=ex(sinx﹣cosx)(0≤x≤2016π),则函数f(x)的各极大值之和为( )
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】D
【解析】解::∵函数f(x)=ex(sinx﹣cosx),
∴f′(x)=[ex(sinx﹣cosx)]′=ex(sinx﹣cosx)+ex(cosx+sinx)=2exsinx;
令f′(x)=0,解得x=kπ(k∈Z);
∴当2kπ<x<2kπ+π时,f′(x)>0,原函数单调递增,
当2kπ+π<x<2kπ+2π时,f′(x)<0,原函数单调递减;
∴当x=2kπ+π时,函数f(x)取得极大值,
此时f(2kπ+π)=e2kπ+π[sin(2kπ+π)﹣cos(2kπ+π)]=e2kπ+π;
又∵0≤x≤2016π,∴0和2016π都不是极值点,
∴函数f(x)的各极大值之和为:
eπ+e3π+e5π+…+e2015π= ![]() ,
,
所以答案是:D.
【考点精析】认真审题,首先需要了解函数的极值与导数(求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值).
是极小值).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市郊区有一加油站,2018年初汽油的存储量为50吨,计划从年初起每周初均购进汽油
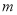 吨,以满足城区内和城外汽车用油需求,已知城外汽车用油每周5吨;城区内汽车用油前
吨,以满足城区内和城外汽车用油需求,已知城外汽车用油每周5吨;城区内汽车用油前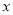 个周需求量
个周需求量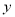 吨与
吨与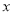 的函数关系式为
的函数关系式为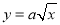
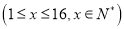 ,
, 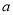 为常数,且前4个周城区内汽车的汽油需求量为100吨.
为常数,且前4个周城区内汽车的汽油需求量为100吨.(1)试写出第
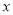 个周结束时,汽油存储量
个周结束时,汽油存储量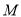 (吨)与
(吨)与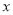 的函数关系式;
的函数关系式;(2)要使16个周内每周按计划购进汽油之后,加油站总能满足城区内和城外的需求,且每周结束时加油站的汽油存储量不超过150吨,试确定
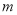 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
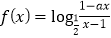 为奇函数,
为奇函数,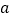 为实常数.
为实常数.(1)求
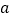 的值;
的值;(2)证明:
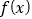 在区间
在区间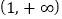 内单调递增;
内单调递增;(3)若对于区间
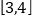 上的每一个
上的每一个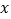 的值,不等式
的值,不等式 恒成立,求实数
恒成立,求实数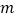 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图动直线l:y=b与抛物线y2=4x交于点A,与椭圆
 =1交于抛物线右侧的点B,F为抛物线的焦点,则|AF|+|BF|+|AB|的最大值为( )
=1交于抛物线右侧的点B,F为抛物线的焦点,则|AF|+|BF|+|AB|的最大值为( )
A.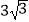
B.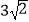
C.2
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c分别为△ABC三个内角A,B,C的对边,ccosA+
 csinA﹣b﹣a=0.
csinA﹣b﹣a=0.
(Ⅰ)求C;
(Ⅱ)若c=1,求△ABC的面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】数列{an}的前n项和记为Sn , a1=2,an+1=Sn+2(n∈N*).
(Ⅰ)求{an}的通项公式;
(Ⅱ)求数列{nan}的前n项和Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
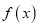 对任意实数
对任意实数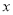 均有
均有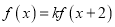 ,其中常数
,其中常数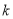 为负数,且
为负数,且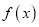 在区间
在区间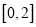 上有表达式
上有表达式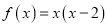 .
.(1)写出
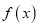 在
在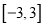 上的表达式,并写出函数
上的表达式,并写出函数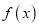 在
在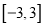 上的单调区间(不用过程,直接写出即可);
上的单调区间(不用过程,直接写出即可);(2)求出
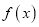 在
在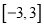 上的最小值与最大值,并求出相应的自变量的取值.
上的最小值与最大值,并求出相应的自变量的取值.
相关试题

