【题目】在平面直角坐标系xOy中,点M到点F(1,0)的距离比它到y轴的距离多1,记点M的轨迹为C.
(1)求轨迹C的方程;
(2)设斜率为k的直线l过定点P(﹣2,1),求直线l与轨迹C恰好有一个公共点、两个公共点、三个公共点时k的相应取值范围.
参考答案:
【答案】
(1)解:设M(x,y),依题意得:|MF|=|x|+1,即 ![]() ,
,
化简得,y2=2|x|+2x.
∴点M的轨迹C的方程为 ![]() ;
;
(2)解:在点M的轨迹C中,记C1:y2=4x(x≥0),C2:y=0(x<0).
依题意,可设直线l的方程为y﹣1=k(x+2).
由方程组 ![]() ,可得ky2﹣4y+4(2k+1)=0.
,可得ky2﹣4y+4(2k+1)=0.
①当k=0时,此时y=1,把y=1代入轨迹C的方程,得 ![]() .
.
故此时直线l:y=1与轨迹C恰好有一个公共点( ![]() ).
).
②当k≠0时,方程ky2﹣4y+4(2k+1)=0的判别式为△=﹣16(2k2+k﹣1).
设直线l与x轴的交点为(x0,0),
则由y﹣1=k(x+2),取y=0得 ![]() .
.
若  ,解得k<﹣1或k>
,解得k<﹣1或k> ![]() .
.
即当k∈ ![]() 时,直线l与C1没有公共点,与C2有一个公共点,
时,直线l与C1没有公共点,与C2有一个公共点,
故此时直线l与轨迹C恰好有一个公共点.
若 ![]() 或
或 ![]() ,解得k=﹣1或k=
,解得k=﹣1或k= ![]() 或
或 ![]() .
.
即当k=﹣1或k= ![]() 时,直线l与C1只有一个公共点,与C2有一个公共点.
时,直线l与C1只有一个公共点,与C2有一个公共点.
当 ![]() 时,直线l与C1有两个公共点,与C2无公共点.
时,直线l与C1有两个公共点,与C2无公共点.
故当k=﹣1或k= ![]() 或
或 ![]() 时,直线l与轨迹C恰好有两个公共点.
时,直线l与轨迹C恰好有两个公共点.
若  ,解得﹣1<k<﹣
,解得﹣1<k<﹣ ![]() 或0<k<
或0<k< ![]() .
.
即当﹣1<k<﹣ ![]() 或0<k<
或0<k< ![]() 时,直线l与C1有两个公共点,与C2有一个公共点.
时,直线l与C1有两个公共点,与C2有一个公共点.
此时直线l与C恰有三个公共点.
综上,当k∈ ![]() ∪{0}时,直线l与C恰有一个公共点;
∪{0}时,直线l与C恰有一个公共点;
当k ![]() ∪{﹣1,
∪{﹣1, ![]() }时,直线l与C恰有两个公共点;
}时,直线l与C恰有两个公共点;
当k∈ ![]() 时,直线l与轨迹C恰有三个公共点.
时,直线l与轨迹C恰有三个公共点.
【解析】(1)设出M点的坐标,直接由题意列等式,整理后即可得到M的轨迹C的方程;(2)设出直线l的方程为y﹣1=k(x+2),和(1)中的轨迹方程联立化为关于y的一元二次方程,求出判别式,再在直线y﹣1=k(x+2)中取y=0得到 ![]() .然后分判别式小于0、等于0、大于0结合x0<0求解使直线l与轨迹C恰好有一个公共点、两个公共点、三个公共点时k的相应取值范围.
.然后分判别式小于0、等于0、大于0结合x0<0求解使直线l与轨迹C恰好有一个公共点、两个公共点、三个公共点时k的相应取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校举办的集体活动中,设计了如下有奖闯关游戏:参赛选手按第一关、第二关、第三关的顺序依次闯关,若闯关成功,分别获得1分、2分、3分的奖励,游戏还规定,当选手闯过一关后,可以选择得到相应的分数,结束游戏;也可以选择继续闯下一关,若有任何一关没有闯关成功,则全部分数都归零,游戏结束。设选手甲第一关、第二关、第三关的概率分别为
 ,
, ,
, ,选手选择继续闯关的概率均为
,选手选择继续闯关的概率均为 ,且各关之间闯关成功互不影响
,且各关之间闯关成功互不影响(I)求选手甲第一关闯关成功且所得分数为零的概率
(II)设该学生所得总分数为X,求X的分布列与数学期望
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
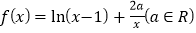 .
.(1)求
 的单调区间;
的单调区间;(2)如果当
 ,且
,且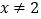 时,
时,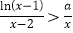 恒成立,求实数
恒成立,求实数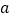 的范围.
的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】学校计划在全国中学生田径比赛期间,安排6位志愿者到4个比赛场地提供服务,要求甲、乙两个比赛场地各安排一个人,剩下两个比赛场地各安排两个人,其中的小李和小王不在一起,不同的安排方案共有( )
A. 168种 B. 156种 C. 172种 D. 180种
-
科目: 来源: 题型:
查看答案和解析>>【题目】π为圆周率,e=2.71828…为自然对数的底数.
(1)求函数f(x)= 的单调区间;
的单调区间;
(2)求e3 , 3e , eπ , πe , 3π , π3这6个数中的最大数和最小数;
(3)将e3 , 3e , eπ , πe , 3π , π3这6个数按从小到大的顺序排列,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】不等式组
 的解集记为D,有下列四个命题:
的解集记为D,有下列四个命题:
p1:(x,y)∈D,x+2y≥﹣2 p2:(x,y)∈D,x+2y≥2
p3:(x,y)∈D,x+2y≤3 p4:(x,y)∈D,x+2y≤﹣1
其中真命题是( )
A.p2 , p3
B.p1 , p4
C.p1 , p2
D.p1 , p3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱
 中,
中, ,
, 为棱
为棱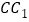 的中点,
的中点, .
.
(1)证明:
 平面
平面 ;
;(2)设二面角
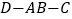 的正切值为
的正切值为 ,
, ,
, ,求异面直线
,求异面直线 与
与 所成角的余弦值.
所成角的余弦值.
相关试题

