【题目】选修4-4:坐标系与参数方程
已知圆锥曲线![]() (
(![]() 为参数)和定点
为参数)和定点![]() ,
,![]() 、
、![]() 是此圆锥曲线的左、右焦点,以原点
是此圆锥曲线的左、右焦点,以原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求直线![]() 的直角坐标方程;
的直角坐标方程;
(2)经过点![]() 且与直线
且与直线![]() 垂直的直线
垂直的直线![]() 交此圆锥曲线于
交此圆锥曲线于![]() 、
、![]() 两点,求
两点,求![]() 的值.
的值.
参考答案:
【答案】(1) ![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)将曲线![]() 的参数方程
的参数方程![]() 化为普通方程得
化为普通方程得![]() ,由此先求出焦点坐标,由直线的截距式求出直线方程即可;(2)由(1)知,直线
,由此先求出焦点坐标,由直线的截距式求出直线方程即可;(2)由(1)知,直线![]() 的斜率为
的斜率为![]() ,因为
,因为![]() ,所以
,所以![]() 的斜率为
的斜率为![]() ,所可写出直线
,所可写出直线![]() 的参数方程,将其参数方程代入椭圆方程,由直线参数的几何意义求之即可.
的参数方程,将其参数方程代入椭圆方程,由直线参数的几何意义求之即可.
试题解析:(1)曲线![]() 可化为
可化为![]() ,
,
其轨迹为椭圆,焦点为![]() ,
,![]() .
.
经过![]() 和
和![]() 的直线方程为
的直线方程为![]() ,即
,即![]() .
.
(2)由(1)知,直线![]() 的斜率为
的斜率为![]() ,因为
,因为![]() ,所以
,所以![]() 的斜率为
的斜率为![]() ,倾斜角为
,倾斜角为![]() ,
,
所以![]() 的参数方程为
的参数方程为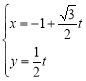 (
(![]() 为参数).
为参数).
代入椭圆![]() 的方程中,得
的方程中,得![]() .
.
因为![]() 在点
在点![]() 的两侧,所以
的两侧,所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某小区拟在空地上建一个占地面积为2400平方米的矩形休闲广场,按照设计要求,休闲广场中间有两个完全相同的矩形绿化区域,周边及绿化区域之间是道路(图中阴影部分),道路的宽度均为2米.怎样设计矩形休闲广场的长和宽,才能使绿化区域的总面积最大?并求出其最大面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
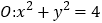 ,圆
,圆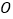 与
与 轴交于
轴交于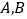 两点,过点
两点,过点 的圆的切线为
的圆的切线为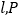 是圆上异于
是圆上异于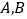 的一点,
的一点, 垂直于
垂直于 轴,垂足为
轴,垂足为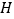 ,
,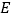 是
是 的中点,延长
的中点,延长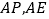 分别交
分别交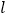 于
于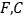 .
.
(1)若点
 ,求以
,求以 为直径的圆的方程,并判断
为直径的圆的方程,并判断 是否在圆上;
是否在圆上;(2)当
 在圆上运动时,证明:直线
在圆上运动时,证明:直线 恒与圆
恒与圆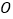 相切.
相切. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校男女篮球队各有10名队员,现将这20名队员的身高绘制成茎叶图(单位:
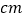 ).男队员身高在
).男队员身高在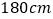 以上定义为“高个子”,女队员身高在
以上定义为“高个子”,女队员身高在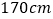 以上定义为“高个子”,其他队员定义为“非高个子”,按照“高个子”和“非高个子”用分层抽样的方法共抽取5名队员.
以上定义为“高个子”,其他队员定义为“非高个子”,按照“高个子”和“非高个子”用分层抽样的方法共抽取5名队员.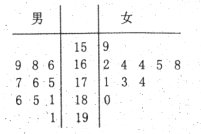
(1)从这5名队员中随机选出2名队员,求这2名队员中有“高个子”的概率;
(2)求这5名队员中,恰好男女“高个子”各1名队员的概率.
-
科目: 来源: 题型:
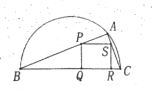
查看答案和解析>>【题目】如图,某市园林局准备绿化一块直径为
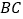 的半圆空地,
的半圆空地,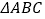 以外的地方种草,
以外的地方种草,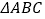 的内接正方形
的内接正方形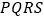 为一水池,其余的地方种花,若
为一水池,其余的地方种花,若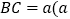 为定值),
为定值),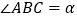 ,设
,设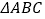 的面积为
的面积为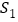 ,正方形
,正方形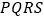 的面积为
的面积为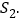
(1)用
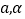 表示
表示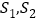 ;
;(2)当
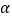 为何值时,
为何值时,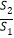 取得最大值,并求出此最大值.
取得最大值,并求出此最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的几何体中,四边形
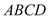 为矩形,直线
为矩形,直线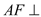 平面
平面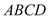 ,
,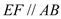 ,
,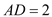 ,
, ,点
,点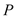 在棱
在棱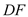 上.
上.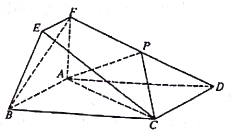
(1)求证:
 ;
;(2)若
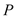 是
是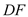 的中点,求异面直线
的中点,求异面直线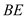 与
与 所成角的余弦值;
所成角的余弦值;(3)若


 ,求二面角
,求二面角 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售某件商品的经验表明,该商品每日的销量
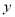 (单位:千克)与销售价格
(单位:千克)与销售价格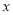 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式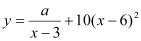 ,其中
,其中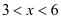 ,
,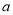 为常数。已知销售价格为5元/千克时,每日可售出该商品11千克。
为常数。已知销售价格为5元/千克时,每日可售出该商品11千克。(Ⅰ)求实数
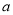 的值;
的值;(Ⅱ)若该商品的成本为3元/千克,试确定销售价格
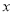 的值,使商场每日销售该商品所获得的利润最大。
的值,使商场每日销售该商品所获得的利润最大。
相关试题

