【题目】如图,某小区拟在空地上建一个占地面积为2400平方米的矩形休闲广场,按照设计要求,休闲广场中间有两个完全相同的矩形绿化区域,周边及绿化区域之间是道路(图中阴影部分),道路的宽度均为2米.怎样设计矩形休闲广场的长和宽,才能使绿化区域的总面积最大?并求出其最大面积.

参考答案:
【答案】当休闲广场的长为![]() 米,宽为
米,宽为![]() 米时,绿化区域总面积最大值,最大面积为
米时,绿化区域总面积最大值,最大面积为![]() 平方米.
平方米.
【解析】试题分析:设矩形休闲广场的长为x米,根据占地面积表示出宽,结合道路的宽度均为2米,求出绿化区域的面积表达式,结合基本不等式可得答案
试题解析:设矩形休闲广场的长为x米,依题意,其宽为![]() 米, 绿化区域的面积为
米, 绿化区域的面积为
![]() ,
,![]()
![]()
![]()
当且仅当![]() 即
即![]() 时取等号,此时
时取等号,此时![]()
所以,当矩形休闲广场的长为60米和宽为40米时,才能使绿化区域的总面积最大,最大面积为1944平方米
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义在
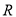 上的单调递减函数
上的单调递减函数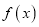 ,对任意
,对任意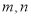 都有
都有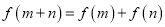 ,
,  .
.(Ⅰ)判断函数
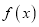 的奇偶性,并证明之;
的奇偶性,并证明之;(Ⅱ)若对任意
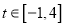 ,不等式
,不等式 (
( 为常实数)都成立,求
为常实数)都成立,求 的取值范围;(Ⅲ)设
的取值范围;(Ⅲ)设 ,
,  ,
,  ,
, 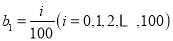 ,
,  .
.若

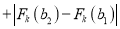
 ,
,  ,比较
,比较 的大小并说明理由.
的大小并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
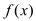 的定义域为[-1,5],部分对应值如下表,
的定义域为[-1,5],部分对应值如下表,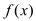 的导函数
的导函数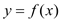 的图象如图所示,下列关于
的图象如图所示,下列关于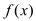 的命题:
的命题: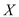
-1
0
4
5
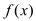
1
2
2
1
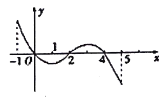
①函数
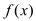 的极大值点为0,4;
的极大值点为0,4;②函数
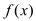 在[0,2]上是减函数;
在[0,2]上是减函数;③如果当
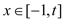 时,
时,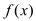 的最大值是2,那么
的最大值是2,那么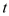 的最大值为4;
的最大值为4;④当
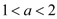 时,函数
时,函数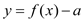 有4个零点.
有4个零点.其中正确命题的序号是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直四棱柱
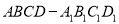 中,底面
中,底面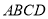 为等腰梯形,
为等腰梯形, 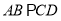 ,
, 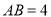 ,
, 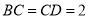 ,
, 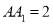 ,
, 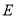 、
、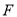 、
、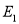 分别是棱
分别是棱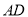 、
、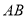 、
、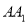 的中点.
的中点.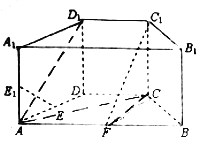
(1)证明:直线
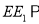 平面
平面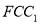 ;
;(2)求证:面
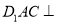 面
面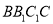 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
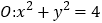 ,圆
,圆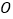 与
与 轴交于
轴交于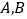 两点,过点
两点,过点 的圆的切线为
的圆的切线为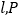 是圆上异于
是圆上异于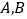 的一点,
的一点, 垂直于
垂直于 轴,垂足为
轴,垂足为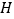 ,
,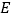 是
是 的中点,延长
的中点,延长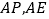 分别交
分别交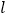 于
于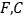 .
.
(1)若点
 ,求以
,求以 为直径的圆的方程,并判断
为直径的圆的方程,并判断 是否在圆上;
是否在圆上;(2)当
 在圆上运动时,证明:直线
在圆上运动时,证明:直线 恒与圆
恒与圆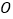 相切.
相切. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校男女篮球队各有10名队员,现将这20名队员的身高绘制成茎叶图(单位:
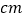 ).男队员身高在
).男队员身高在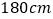 以上定义为“高个子”,女队员身高在
以上定义为“高个子”,女队员身高在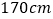 以上定义为“高个子”,其他队员定义为“非高个子”,按照“高个子”和“非高个子”用分层抽样的方法共抽取5名队员.
以上定义为“高个子”,其他队员定义为“非高个子”,按照“高个子”和“非高个子”用分层抽样的方法共抽取5名队员.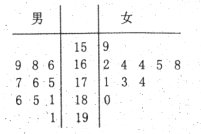
(1)从这5名队员中随机选出2名队员,求这2名队员中有“高个子”的概率;
(2)求这5名队员中,恰好男女“高个子”各1名队员的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知圆锥曲线
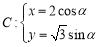 (
(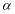 为参数)和定点
为参数)和定点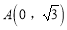 ,
,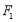 、
、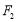 是此圆锥曲线的左、右焦点,以原点
是此圆锥曲线的左、右焦点,以原点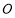 为极点,以
为极点,以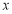 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.(1)求直线
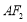 的直角坐标方程;
的直角坐标方程;(2)经过点
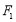 且与直线
且与直线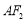 垂直的直线
垂直的直线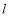 交此圆锥曲线于
交此圆锥曲线于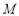 、
、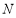 两点,求
两点,求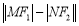 的值.
的值.
相关试题

