【题目】某商场销售某件商品的经验表明,该商品每日的销量![]() (单位:千克)与销售价格
(单位:千克)与销售价格![]() (单位:元/千克)满足关系式
(单位:元/千克)满足关系式![]() ,其中
,其中![]() ,
,![]() 为常数。已知销售价格为5元/千克时,每日可售出该商品11千克。
为常数。已知销售价格为5元/千克时,每日可售出该商品11千克。
(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)若该商品的成本为3元/千克,试确定销售价格![]() 的值,使商场每日销售该商品所获得的利润最大。
的值,使商场每日销售该商品所获得的利润最大。
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)当销售价格为4元/千克时,商场每日销售该商品所获得的利润最大.
;(Ⅱ)当销售价格为4元/千克时,商场每日销售该商品所获得的利润最大.
【解析】
试题分析:(Ⅰ)因为销售价格为5元/千克时,每日可售出该商品11千克即为![]() 时,
时,![]() 代入解析式可求得a;(Ⅱ)本小题考查用导数方法解决函数最值问题,先求出函数的导数,列表分析导函数在各部分区间内的单调情况,找到极值点,同时要注意函数的定义域.
代入解析式可求得a;(Ⅱ)本小题考查用导数方法解决函数最值问题,先求出函数的导数,列表分析导函数在各部分区间内的单调情况,找到极值点,同时要注意函数的定义域.
试题解析:(Ⅰ)根据题意可得,当![]() 时,
时,![]() ,代入解析式得:
,代入解析式得:![]() ,所以
,所以![]() ;
;
(Ⅱ)因为![]() ,所以该商品每日销售量为:
,所以该商品每日销售量为:
![]()
每日销售该商品所获得的利润为:
![]()
![]() ,
,![]()
所以![]()
![]()
所以,![]() 的变化情况如下表:
的变化情况如下表:
| (3,4) | 4 | (4,6) |
| + | 0 | - |
| 递增 | 极大值42 | 递减 |
由上表可得,![]() 是函数在区间(3,6)上的极大值点,也是最大值点;
是函数在区间(3,6)上的极大值点,也是最大值点;
所以当![]() 时,函数
时,函数![]() 取得最大值42;
取得最大值42;
因此,当销售价格为4元/千克时,商场每日销售该商品所获得的利润最大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知圆锥曲线
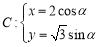 (
(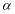 为参数)和定点
为参数)和定点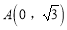 ,
,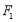 、
、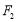 是此圆锥曲线的左、右焦点,以原点
是此圆锥曲线的左、右焦点,以原点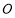 为极点,以
为极点,以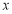 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.(1)求直线
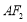 的直角坐标方程;
的直角坐标方程;(2)经过点
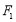 且与直线
且与直线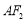 垂直的直线
垂直的直线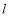 交此圆锥曲线于
交此圆锥曲线于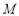 、
、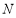 两点,求
两点,求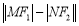 的值.
的值. -
科目: 来源: 题型:
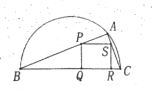
查看答案和解析>>【题目】如图,某市园林局准备绿化一块直径为
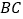 的半圆空地,
的半圆空地,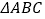 以外的地方种草,
以外的地方种草,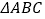 的内接正方形
的内接正方形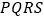 为一水池,其余的地方种花,若
为一水池,其余的地方种花,若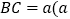 为定值),
为定值),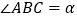 ,设
,设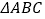 的面积为
的面积为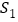 ,正方形
,正方形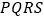 的面积为
的面积为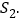
(1)用
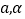 表示
表示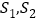 ;
;(2)当
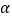 为何值时,
为何值时,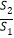 取得最大值,并求出此最大值.
取得最大值,并求出此最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的几何体中,四边形
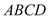 为矩形,直线
为矩形,直线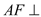 平面
平面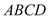 ,
,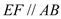 ,
,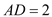 ,
, ,点
,点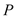 在棱
在棱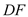 上.
上.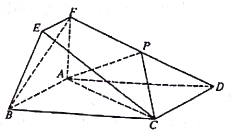
(1)求证:
 ;
;(2)若
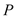 是
是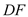 的中点,求异面直线
的中点,求异面直线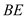 与
与 所成角的余弦值;
所成角的余弦值;(3)若


 ,求二面角
,求二面角 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了传承经典,促进学生课外阅读,某校从高中年级和初中年级各随机抽取100名学生进行有关对中国四大名著常识了解的竞赛.图1和图2分别是高中年级和初中年级参加竞赛的学生成绩按照
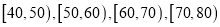 分组,得到的频率分布直方图.
分组,得到的频率分布直方图.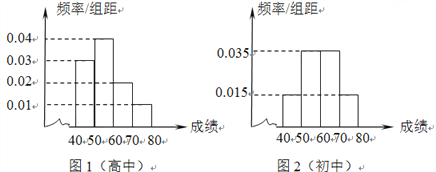
(1)分别计算参加这次知识竞赛的两个学段的学生的平均成绩;
(2)规定竞赛成绩达到
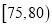 为优秀,经统计初中年级有3名男同学,2名女同学达到优秀,现从上述5人中任选两人参加复试,求选中的2人恰好都为女生的概率;
为优秀,经统计初中年级有3名男同学,2名女同学达到优秀,现从上述5人中任选两人参加复试,求选中的2人恰好都为女生的概率;(3)完成下列
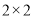 的列联表,并回答是否有99%的把握认为“两个学段的学生对四大名著的了解有差异”?
的列联表,并回答是否有99%的把握认为“两个学段的学生对四大名著的了解有差异”?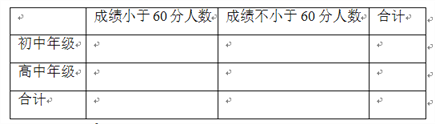
附:
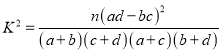
临界值表:
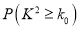
0.10
0.05
0.01
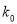
2.706
3.841
6.635
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于函数
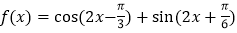 ,有下列结论:
,有下列结论:①
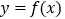 的最大值为
的最大值为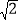 ;
;②
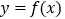 的最小正周期是
的最小正周期是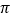 ;
;③
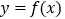 在区间
在区间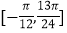 上是减函数;
上是减函数;④直线
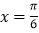 是函数
是函数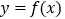 的一条对称轴方程.
的一条对称轴方程.其中正确结论的序号是__________.
-
科目: 来源: 题型:
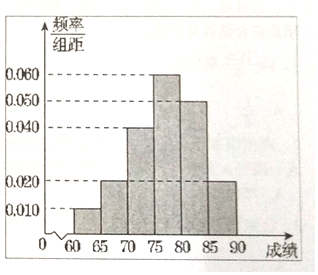
查看答案和解析>>【题目】在某次综合素质测试中,共设有60个考场,每个考场30名考生,在考试结束后,为调查其测试前的培训辅导情况与测试成绩的相关性,抽取每个考场中座位号为06的考生,统计了他们的成绩,得到如图所示的频率分布直方图.
问:
在这个调查采样中,采用的是什么抽样方法?
估计这次测试中优秀(80分及以上)的人数;
写出这60名考生成绩的众数、中位数、平均数的估计值.
相关试题

