【题目】如图,某市园林局准备绿化一块直径为![]() 的半圆空地,
的半圆空地,![]() 以外的地方种草,
以外的地方种草,![]() 的内接正方形
的内接正方形![]() 为一水池,其余的地方种花,若
为一水池,其余的地方种花,若![]() 为定值),
为定值),![]() ,设
,设![]() 的面积为
的面积为![]() ,正方形
,正方形![]() 的面积为
的面积为![]()
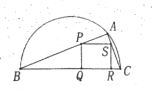
(1)用![]() 表示
表示![]() ;
;
(2)当![]() 为何值时,
为何值时,![]() 取得最大值,并求出此最大值.
取得最大值,并求出此最大值.
参考答案:
【答案】(1) ![]()
![]() ;(2)
;(2) ![]() 的最大值为
的最大值为![]() ,此时
,此时![]() .
.
【解析】试题分析:(1)在Rt△ABC中,BC=a,∠ABC=α,由AB=acosα,AC=asinα,能求出S1;设正方形PQRS的边长为x,则BP=![]() ,AP=xcosα,由BP+AP=
,AP=xcosα,由BP+AP=![]() ,AB=acosα,AP+BP=AB,能求出S2.
,AB=acosα,AP+BP=AB,能求出S2.
(2)![]() =
=![]() ,令sin2α=t,推导出
,令sin2α=t,推导出![]() =
=![]() ,0<t≤1,设f(t)=
,0<t≤1,设f(t)=![]() (0<t≤1),推导出f(t)=
(0<t≤1),推导出f(t)=![]() 在(0,1]上单调递减,由此能求出
在(0,1]上单调递减,由此能求出![]() 的最大值及相应的α.
的最大值及相应的α.
试题解析:
(1)在![]() 中,
中,![]() ,
,
所以![]()
设正方形![]() 的边长为
的边长为![]() ,则
,则![]()
由![]()
![]() 又
又![]()
![]()
所以![]()
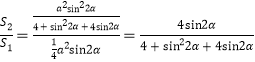
令![]() ,由
,由![]() 得
得![]() ,所以
,所以![]()
![]()
![]()
设![]() ,任取
,任取![]() ,
,
则![]()
![]() 在
在![]() 上单调减,所以
上单调减,所以![]() ,
,
所以![]()
所以![]() 的最大值为
的最大值为![]() ,此时
,此时![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
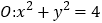 ,圆
,圆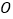 与
与 轴交于
轴交于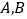 两点,过点
两点,过点 的圆的切线为
的圆的切线为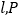 是圆上异于
是圆上异于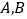 的一点,
的一点, 垂直于
垂直于 轴,垂足为
轴,垂足为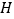 ,
,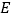 是
是 的中点,延长
的中点,延长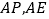 分别交
分别交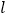 于
于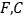 .
.
(1)若点
 ,求以
,求以 为直径的圆的方程,并判断
为直径的圆的方程,并判断 是否在圆上;
是否在圆上;(2)当
 在圆上运动时,证明:直线
在圆上运动时,证明:直线 恒与圆
恒与圆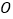 相切.
相切. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校男女篮球队各有10名队员,现将这20名队员的身高绘制成茎叶图(单位:
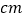 ).男队员身高在
).男队员身高在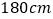 以上定义为“高个子”,女队员身高在
以上定义为“高个子”,女队员身高在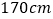 以上定义为“高个子”,其他队员定义为“非高个子”,按照“高个子”和“非高个子”用分层抽样的方法共抽取5名队员.
以上定义为“高个子”,其他队员定义为“非高个子”,按照“高个子”和“非高个子”用分层抽样的方法共抽取5名队员.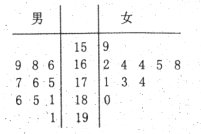
(1)从这5名队员中随机选出2名队员,求这2名队员中有“高个子”的概率;
(2)求这5名队员中,恰好男女“高个子”各1名队员的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知圆锥曲线
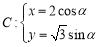 (
(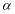 为参数)和定点
为参数)和定点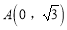 ,
,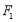 、
、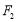 是此圆锥曲线的左、右焦点,以原点
是此圆锥曲线的左、右焦点,以原点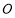 为极点,以
为极点,以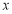 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.(1)求直线
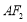 的直角坐标方程;
的直角坐标方程;(2)经过点
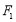 且与直线
且与直线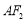 垂直的直线
垂直的直线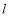 交此圆锥曲线于
交此圆锥曲线于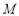 、
、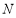 两点,求
两点,求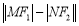 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的几何体中,四边形
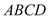 为矩形,直线
为矩形,直线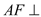 平面
平面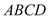 ,
,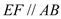 ,
,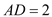 ,
, ,点
,点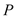 在棱
在棱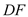 上.
上.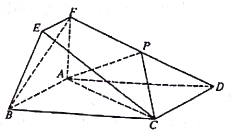
(1)求证:
 ;
;(2)若
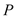 是
是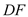 的中点,求异面直线
的中点,求异面直线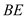 与
与 所成角的余弦值;
所成角的余弦值;(3)若


 ,求二面角
,求二面角 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售某件商品的经验表明,该商品每日的销量
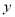 (单位:千克)与销售价格
(单位:千克)与销售价格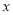 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式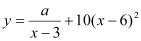 ,其中
,其中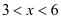 ,
,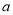 为常数。已知销售价格为5元/千克时,每日可售出该商品11千克。
为常数。已知销售价格为5元/千克时,每日可售出该商品11千克。(Ⅰ)求实数
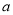 的值;
的值;(Ⅱ)若该商品的成本为3元/千克,试确定销售价格
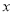 的值,使商场每日销售该商品所获得的利润最大。
的值,使商场每日销售该商品所获得的利润最大。 -
科目: 来源: 题型:
查看答案和解析>>【题目】为了传承经典,促进学生课外阅读,某校从高中年级和初中年级各随机抽取100名学生进行有关对中国四大名著常识了解的竞赛.图1和图2分别是高中年级和初中年级参加竞赛的学生成绩按照
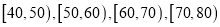 分组,得到的频率分布直方图.
分组,得到的频率分布直方图.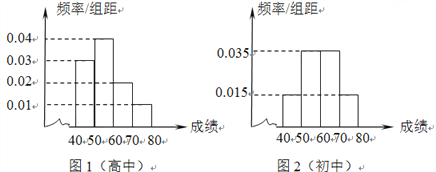
(1)分别计算参加这次知识竞赛的两个学段的学生的平均成绩;
(2)规定竞赛成绩达到
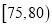 为优秀,经统计初中年级有3名男同学,2名女同学达到优秀,现从上述5人中任选两人参加复试,求选中的2人恰好都为女生的概率;
为优秀,经统计初中年级有3名男同学,2名女同学达到优秀,现从上述5人中任选两人参加复试,求选中的2人恰好都为女生的概率;(3)完成下列
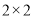 的列联表,并回答是否有99%的把握认为“两个学段的学生对四大名著的了解有差异”?
的列联表,并回答是否有99%的把握认为“两个学段的学生对四大名著的了解有差异”?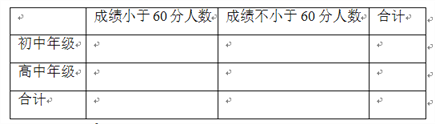
附:
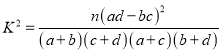
临界值表:
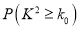
0.10
0.05
0.01
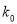
2.706
3.841
6.635
相关试题

