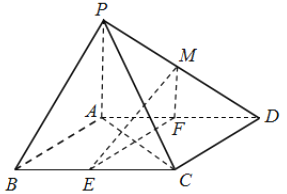
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形, ![]() ,侧面
,侧面![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上.
上.
(1)求证: ![]() 平面
平面![]() ;
;
(2)如果直线![]() 与平面
与平面![]() 所成的角和直线
所成的角和直线![]() 与平面
与平面![]() 所成的角相等,求
所成的角相等,求![]() 的值.
的值.
参考答案:
【答案】(1)证明见解析(2)![]() .
.
【解析】试题分析:
(Ⅰ)在平行四边形![]() 中,由条件可得
中,由条件可得![]() ,进而可得
,进而可得![]() 。由侧面
。由侧面![]() 底面
底面![]() ,得
,得![]() 底面
底面![]() ,故得
,故得![]() ,所以可证得
,所以可证得![]() 平面
平面![]() .(Ⅱ)先证明平面
.(Ⅱ)先证明平面![]() 平面
平面![]() ,由面面平行的性质可得
,由面面平行的性质可得![]() 平面
平面![]() .(Ⅲ)建立空间直角坐标系,通过求出平面的法向量,根据线面角的向量公式可得
.(Ⅲ)建立空间直角坐标系,通过求出平面的法向量,根据线面角的向量公式可得![]() 。
。
试题解析:
(Ⅰ)证明:在平行四边形![]() 中,
中,
∵![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,
∵侧面![]() 底面
底面![]() ,且
,且![]() ,
,
∴![]() 底面
底面![]() ,
,
又![]() 底面
底面![]() ,
,
∴![]() ,
,
又![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(Ⅱ)证明:∵![]() 为
为![]() 的中点,
的中点, ![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
同理![]() 平面
平面![]() ,
,
又![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(Ⅲ)解:由![]() 底面
底面![]() ,
, ![]() ,可得
,可得![]() ,
, ![]() ,
, ![]() 两两垂直,
两两垂直,
建立如图空间直角坐标系![]() ,
,

则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
所以![]() ,
, ![]() ,
, ![]() ,
,
设![]() ,则
,则![]() ,
,
∴![]() ,
, ![]() ,
,
易得平面![]() 的法向量
的法向量![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则:
,则:
由![]() ,得
,得![]() ,
,
令![]() ,得
,得![]() ,
,
∵直线![]() 与平面
与平面![]() 所成的角和此直线与平面
所成的角和此直线与平面![]() 所成的角相等,
所成的角相等,
∴![]() ,即
,即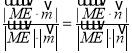 ,
,
∴![]() ,
,
解得![]() 或
或![]() (舍去),
(舍去),
故![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标
 中,圆
中,圆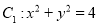 ,圆
,圆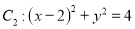 。
。(Ⅰ)在以O为极点,x轴正半轴为极轴的极坐标系中,分别写出圆
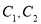 的极坐标方程,并求出圆
的极坐标方程,并求出圆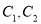 的交点坐标(用极坐标表示);
的交点坐标(用极坐标表示);(Ⅱ)求圆
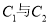 的公共弦的参数方程。
的公共弦的参数方程。 -
科目: 来源: 题型:
查看答案和解析>>【题目】若对任意
 ,
,  有唯一确定的
有唯一确定的 与之对应,则称
与之对应,则称 为关于
为关于 ,
,  的二元函数,现定义满足下列性质的
的二元函数,现定义满足下列性质的 为关于实数
为关于实数 ,
,  的广义“距离”.
的广义“距离”.(
 )非负性:
)非负性:  ,当且仅当
,当且仅当 时取等号;
时取等号;(
 )对称性:
)对称性:  ;
;(
 )三角形不等式:
)三角形不等式:  对任意的实数
对任意的实数 均成立.
均成立.给出三个二元函数:①
 ;②
;② ;③
;③ ,
,则所有能够成为关于
 ,
,  的广义“距离”的序号为__________.
的广义“距离”的序号为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】学校高一年级开设
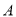 、
、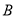 、
、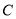 、
、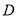 、
、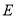 五门选修课,每位同学须彼此独立地选三课程,其中甲同学必选
五门选修课,每位同学须彼此独立地选三课程,其中甲同学必选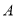 课程,不选
课程,不选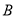 课程,另从其余课程中随机任选两门课程.乙、丙两名同学从五门课程中随机任选三门课程.
课程,另从其余课程中随机任选两门课程.乙、丙两名同学从五门课程中随机任选三门课程.(Ⅰ)求甲同学选中
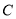 课程且乙同学未选中
课程且乙同学未选中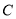 课程的概率.
课程的概率.(Ⅱ)用
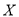 表示甲、乙、丙选中
表示甲、乙、丙选中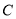 课程的人数之和,求
课程的人数之和,求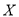 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知常数
 ,向量
,向量 ,
,  ,经过点
,经过点 ,以
,以 为方向向量的直线与经过点
为方向向量的直线与经过点 ,以
,以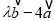 为方向向量的直线交于点
为方向向量的直线交于点 ,其中
,其中 .
.(
 )求点
)求点 的轨迹方程,并指出轨迹
的轨迹方程,并指出轨迹 .
.(
 )若点
)若点 ,当
,当 时,
时,  为轨迹
为轨迹 上任意一点,求
上任意一点,求 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
,  .
.(Ⅰ)当
 时,求曲线
时,求曲线 在点
在点 处的切线方程.
处的切线方程.(Ⅱ)当
 时,若曲线
时,若曲线 上的点
上的点 都在不等式组
都在不等式组 所表示的平面区域内,试求
所表示的平面区域内,试求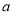 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的右焦点为
的右焦点为 ,右顶点为
,右顶点为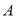 ,离心离为
,离心离为 ,点
,点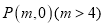 满足条件
满足条件 .
.(Ⅰ)求
 的值.
的值.(Ⅱ)设过点
 的直线
的直线 与椭圆
与椭圆 相交于
相交于 、
、 两点,记
两点,记 和
和 的面积分别为
的面积分别为 、
、 ,求证:
,求证:  .
.
相关试题

