【题目】如图,某种水箱用的“浮球”,是由两个半球和一个圆柱筒组成的.已知半球的直径是6 cm,圆柱筒高为2 cm.

(1)这种“浮球”的体积是多少cm3(结果精确到0.1)?
(2)要在2 500个这样的“浮球”表面涂一层胶,如果每平方米需要涂胶100克,那么共需胶多少克?
参考答案:
【答案】(1) 169.6 (2) 1 200π
【解析】(1)因为半球的直径是6 cm,所以半径R=3 cm,
所以两个半球的体积之和为V球=πR3=π·27=36π(cm3).
又圆柱筒的体积为V圆柱=πR2·h=π×9×2=18π(cm3).
所以这种“浮球”的体积是V=V球+V圆柱=36π+18π=54π≈169.6(cm3).
(2)上下两个半球的表面积是S球表=4πR2=4×π×9=36π(cm2),
又“浮球”的圆柱筒的侧面积为S圆柱侧=2πRh=2×π×3×2=12π(cm2),
所以1个“浮球”的表面积为S==π(m2).
因此2 500个这样的“浮球”的表面积为2 500S=2 500×π=12π(m2).
因为每平方米需要涂胶100克,所以共需要胶的质量为100×12π=
1 200π(克).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为a,E、F、G、H分别为AB、BC、CD、DA的中点.若沿EF、FG、GH、HE将四角折起,试问能折成一个四棱锥吗?为什么?你从中能得到什么结论?对于圆锥有什么类似的结论?

-
科目: 来源: 题型:
查看答案和解析>>【题目】一个几何体,它的下面是一个圆柱,上面是一个圆锥,并且圆锥的底面与圆柱的上底面重合,圆柱的底面直径为3 cm,高为4 cm,圆锥的高为3 cm,画出此几何体的直观图.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A={x|-3≤x<3},B={x|2<x≤5},则A∪B=( )
A.{x|2<x<3}
B.{x|-3≤x≤5}
C.{x|-3<x<5}
D.{x|-3<x≤5} -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
 满足
满足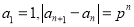 ,其中
,其中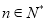 ,
,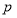 是不为1的常数.
是不为1的常数.(Ⅰ)证明:若
 是递增数列,则
是递增数列,则 不可能是等差数列;
不可能是等差数列;(Ⅱ)证明:若
 是递减的等比数列,则
是递减的等比数列,则 中的每一项都大于其后任意
中的每一项都大于其后任意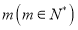 个项的和;
个项的和;(Ⅲ)若
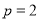 ,且
,且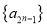 是递增数列,
是递增数列,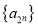 是递减数列,求数列
是递减数列,求数列 的通项公式.
的通项公式. -
科目: 来源: 题型:
查看答案和解析>>【题目】根据统计资料,某工艺品厂的日产量最多不超过20件根据统计资料,每日产品废品率
 与日产量
与日产量 (件)之间近似地满足关系式
(件)之间近似地满足关系式 (日产品废品率=
(日产品废品率= ×100%) .已知每生产一件正品可赢利2千元,而生产一件废品则亏损1千元.(该车间的日利润
×100%) .已知每生产一件正品可赢利2千元,而生产一件废品则亏损1千元.(该车间的日利润 日正品赢利额
日正品赢利额 日废品亏损额)
日废品亏损额) (1)将该车间日利润
 (千元)表示为日产量
(千元)表示为日产量 (件)的函数;
(件)的函数;(2)当该车间的日产量为多少件时,日利润最大?最大日利润是几千元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
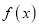 的定义域为
的定义域为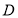 ,若存在闭区间
,若存在闭区间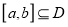 ,使得函数
,使得函数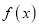 满足:①
满足:①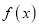 在
在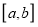
上是单调函数;②
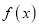 在
在 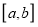 上的值域是
上的值域是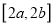 ,则称区间
,则称区间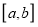 是函数
是函数 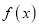 的“和谐区间”,
的“和谐区间”,下列结论错误的是( )
A.函数
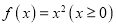 存在 “和谐区间”
存在 “和谐区间”B.函数
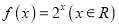 存在 “和谐区间”
存在 “和谐区间”C.函数
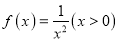 不存在 “和谐区间”
不存在 “和谐区间”D.函数
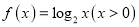 存在 “和谐区间”
存在 “和谐区间”
相关试题

