【题目】选修4-4:坐标系与参数方程
已知曲线![]() 在平面直角坐标系
在平面直角坐标系![]() 下的参数方程为
下的参数方程为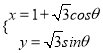 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.
(1)求曲线![]() 的普通方程及极坐标方程;
的普通方程及极坐标方程;
(2)直线![]() 的极坐标方程是
的极坐标方程是![]() ,射线
,射线![]() :
: ![]() 与曲线
与曲线![]() 交于点
交于点![]() 与直线
与直线![]() 交于点
交于点![]() ,求线段
,求线段![]() 的长.
的长.
参考答案:
【答案】(1)![]() ,
, ![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)利用![]() 可消去参数,经圆的参数方程化为普通方程.令
可消去参数,经圆的参数方程化为普通方程.令![]() ,可将圆的普通方程化为极坐标方程.(2)将
,可将圆的普通方程化为极坐标方程.(2)将![]() 分别代入直线的极坐标方程和圆的极坐标方程,可求得
分别代入直线的极坐标方程和圆的极坐标方程,可求得![]() 两点对应的
两点对应的![]() 的值,两者作差即可求得
的值,两者作差即可求得![]() 的长.
的长.
试题解析:(1)因为曲线![]() 的参数方程为
的参数方程为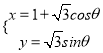 (
(![]() 为参数),
为参数),
消去参数![]() 得曲线
得曲线![]() 的普通方程为
的普通方程为![]() ,
,
又![]() ,
, ![]() ,
,
∴曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(2)由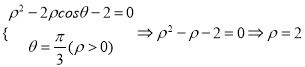 ,
,
故射线![]() 与曲线
与曲线![]() 的交点
的交点![]() 的极坐标为
的极坐标为![]() ;
;
由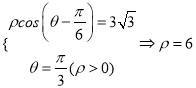 ,
,
故射线![]() 与直线
与直线![]() 的交点
的交点![]() 的极坐标为
的极坐标为![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两支篮球队进行一局比赛,甲获胜的概率为0.6,若采用三局两胜制举行一次比赛,现采用随机模拟的方法估计乙获胜的概率.
先利用计算器或计算机生成0到9之间取整数值的随机数,用0,1,2,3,4,5表示甲获胜;6,7,8,9表示乙获胜,这样能体现甲获胜的概率为0.6.因为采用三局两胜制,所以每3个随机数作为一组.例如,产生30组随机数.
034 743 738 636 964 736 614 698 637 162 332 616 804 560 111 410 959 774 246 762 428 114 572 042 533 237 322 707 360 751
据此估计乙获胜的概率为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
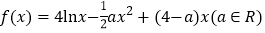 .
.(Ⅰ)讨论
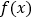 的单调性;
的单调性;(Ⅱ)若函数
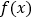 存在极值,对于任意的
存在极值,对于任意的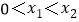 ,存在正实数
,存在正实数 ,使得
,使得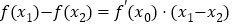 ,试判断
,试判断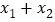 与
与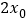 的大小关系并给出证明.
的大小关系并给出证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个学生在一次竞赛中要回答
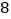 道题是这样产生的:从
道题是这样产生的:从 道物理题中随机抽取
道物理题中随机抽取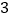 道;从
道;从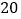 道化学题中随机抽取
道化学题中随机抽取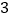 道;从
道;从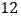 道生物题中随机抽取
道生物题中随机抽取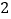 道.使用合适的方法确定这个学生所要回答的三门学科的题的序号(物理题的编号为
道.使用合适的方法确定这个学生所要回答的三门学科的题的序号(物理题的编号为 ,化学题的编号为
,化学题的编号为 ,生物题的编号为
,生物题的编号为 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于定义域为
 的函数
的函数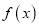 ,若满足①
,若满足①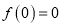 ;②当
;②当 ,且
,且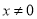 时,都有
时,都有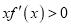 ;③当
;③当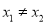 ,且
,且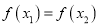 时,
时, 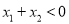 ,则称
,则称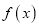 为“偏对函数”.现给出四个函数:
为“偏对函数”.现给出四个函数: 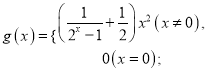
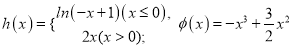 ;
; 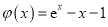 . 则其中是“偏对称函数”的函数个数为( )
. 则其中是“偏对称函数”的函数个数为( )A. 4 B. 3 C. 2 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的右焦点
的右焦点 ,椭圆
,椭圆 的左,右顶点分别为
的左,右顶点分别为 .过点
.过点 的直线
的直线 与椭圆交于
与椭圆交于 两点,且
两点,且 的面积是
的面积是 的面积的3倍.
的面积的3倍. (Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)若
 与
与 轴垂直,
轴垂直, 是椭圆
是椭圆 上位于直线
上位于直线 两侧的动点,且满足
两侧的动点,且满足 ,试问直线
,试问直线 的斜率是否为定值,请说明理由.
的斜率是否为定值,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某种商品在
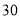 天每件的销售价格
天每件的销售价格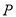 (元)与时间
(元)与时间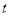 (天)的函数关系用如图表示,该商品在
(天)的函数关系用如图表示,该商品在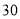 天内日销售量
天内日销售量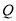 (件)与时间
(件)与时间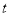 (天)之间的关系如下表:
(天)之间的关系如下表: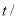 天
天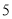
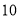
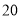
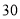
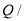 件
件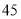
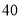
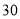
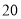

(
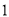 )根据提供的图象(如图),写出该商品每件的销售价格
)根据提供的图象(如图),写出该商品每件的销售价格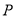 与时间
与时间 的函数关系式.
的函数关系式.(
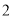 )根据表
)根据表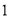 提供的数据,写出日销售量
提供的数据,写出日销售量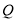 与时间
与时间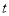 的一次函数关系式.
的一次函数关系式.(
 )求该商品的日销售金额的最大值,并指出日销售金额最大的一天是
)求该商品的日销售金额的最大值,并指出日销售金额最大的一天是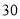 天中的第几天.(日销售金额
天中的第几天.(日销售金额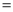 每件的销售价格
每件的销售价格 日销售量)
日销售量)
相关试题

