【题目】对于定义域为![]() 的函数
的函数![]() ,若满足①
,若满足①![]() ;②当
;②当![]() ,且
,且![]() 时,都有
时,都有![]() ;③当
;③当![]() ,且
,且![]() 时,
时, ![]() ,则称
,则称![]() 为“偏对函数”.现给出四个函数:
为“偏对函数”.现给出四个函数: 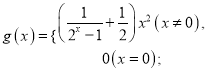
![]() ;
; ![]() . 则其中是“偏对称函数”的函数个数为( )
. 则其中是“偏对称函数”的函数个数为( )
A. 4 B. 3 C. 2 D. 1
参考答案:
【答案】C
【解析】经检验, ![]() 都满足条件①;即条件②等价于函数
都满足条件①;即条件②等价于函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,而容易验证
上单调递增,而容易验证![]() 是奇函数,由及函数的性质可知,
是奇函数,由及函数的性质可知, ![]() 在区间
在区间![]() 和
和![]() 上单调性相同,故
上单调性相同,故![]() 不满足条件②,由复合函数的单调性法则知
不满足条件②,由复合函数的单调性法则知![]() 在区间
在区间![]() 单调递减,显然在
单调递减,显然在![]() 上单调递增,故
上单调递增,故![]() 满足条件②,
满足条件②,![]() 当
当![]() 时,
时, ![]() ,故
,故![]() 不满足条件②,
不满足条件②,![]() ,满足条件②,
,满足条件②,
对于![]() ,不妨设
,不妨设![]() ,则
,则![]() ,
, ![]() ,所以
,所以![]() 满足 ③, 对于
满足 ③, 对于![]() ,
, ![]() ,
, ![]() 在
在![]() 上递减,
上递减, ![]() 在
在![]() 上递增,所以
上递增,所以![]()
![]() ,
, ![]() ,
, ![]() 递增,
递增, ![]() ,不妨设
,不妨设![]() ,则
,则![]() ,
,
![]() ,
, ![]() 所以
所以![]() 满足 ③,所以“偏对称函数”的函数个数为
满足 ③,所以“偏对称函数”的函数个数为![]() . 故选
. 故选![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
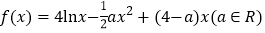 .
.(Ⅰ)讨论
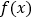 的单调性;
的单调性;(Ⅱ)若函数
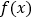 存在极值,对于任意的
存在极值,对于任意的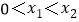 ,存在正实数
,存在正实数 ,使得
,使得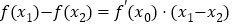 ,试判断
,试判断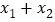 与
与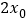 的大小关系并给出证明.
的大小关系并给出证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个学生在一次竞赛中要回答
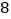 道题是这样产生的:从
道题是这样产生的:从 道物理题中随机抽取
道物理题中随机抽取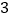 道;从
道;从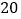 道化学题中随机抽取
道化学题中随机抽取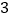 道;从
道;从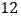 道生物题中随机抽取
道生物题中随机抽取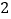 道.使用合适的方法确定这个学生所要回答的三门学科的题的序号(物理题的编号为
道.使用合适的方法确定这个学生所要回答的三门学科的题的序号(物理题的编号为 ,化学题的编号为
,化学题的编号为 ,生物题的编号为
,生物题的编号为 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知曲线
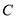 在平面直角坐标系
在平面直角坐标系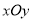 下的参数方程为
下的参数方程为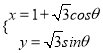 (
(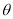 为参数),以坐标原点
为参数),以坐标原点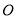 为极点,以
为极点,以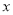 轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.(1)求曲线
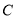 的普通方程及极坐标方程;
的普通方程及极坐标方程;(2)直线
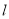 的极坐标方程是
的极坐标方程是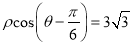 ,射线
,射线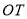 :
: 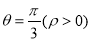 与曲线
与曲线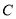 交于点
交于点 与直线
与直线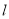 交于点
交于点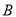 ,求线段
,求线段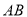 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的右焦点
的右焦点 ,椭圆
,椭圆 的左,右顶点分别为
的左,右顶点分别为 .过点
.过点 的直线
的直线 与椭圆交于
与椭圆交于 两点,且
两点,且 的面积是
的面积是 的面积的3倍.
的面积的3倍. (Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)若
 与
与 轴垂直,
轴垂直, 是椭圆
是椭圆 上位于直线
上位于直线 两侧的动点,且满足
两侧的动点,且满足 ,试问直线
,试问直线 的斜率是否为定值,请说明理由.
的斜率是否为定值,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某种商品在
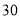 天每件的销售价格
天每件的销售价格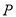 (元)与时间
(元)与时间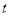 (天)的函数关系用如图表示,该商品在
(天)的函数关系用如图表示,该商品在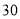 天内日销售量
天内日销售量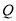 (件)与时间
(件)与时间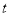 (天)之间的关系如下表:
(天)之间的关系如下表: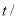 天
天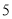
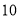
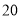
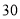
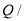 件
件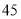
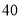
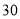

(
 )根据提供的图象(如图),写出该商品每件的销售价格
)根据提供的图象(如图),写出该商品每件的销售价格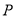 与时间
与时间 的函数关系式.
的函数关系式.(
 )根据表
)根据表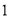 提供的数据,写出日销售量
提供的数据,写出日销售量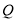 与时间
与时间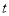 的一次函数关系式.
的一次函数关系式.(
 )求该商品的日销售金额的最大值,并指出日销售金额最大的一天是
)求该商品的日销售金额的最大值,并指出日销售金额最大的一天是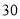 天中的第几天.(日销售金额
天中的第几天.(日销售金额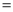 每件的销售价格
每件的销售价格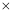 日销售量)
日销售量) -
科目: 来源: 题型:
查看答案和解析>>【题目】定义在
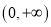 上的函数
上的函数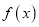 ,如果对任意的
,如果对任意的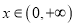 ,都有
,都有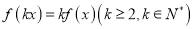 成立,则称
成立,则称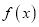 为
为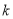 阶伸缩函数.
阶伸缩函数.(
 )若函数
)若函数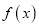 为二阶伸缩函数,且当
为二阶伸缩函数,且当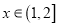 时,
时, 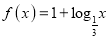 ,求
,求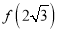 的值.
的值.(
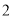 )若
)若 为三阶伸缩函数,且当
为三阶伸缩函数,且当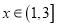 时,
时, 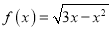 ,求证:函数
,求证:函数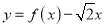 在
在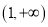 上无零点.
上无零点.(
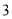 )若函数
)若函数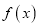 为
为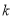 阶伸缩函数,且当
阶伸缩函数,且当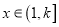 时,
时, 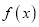 的取值范围是
的取值范围是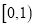 ,求
,求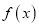 在
在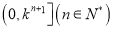 上的取值范围.
上的取值范围.
相关试题

