【题目】已知椭圆![]() 的右焦点
的右焦点![]() ,椭圆
,椭圆![]() 的左,右顶点分别为
的左,右顶点分别为![]() .过点
.过点![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() 两点,且
两点,且![]() 的面积是
的面积是![]() 的面积的3倍.
的面积的3倍.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若![]() 与
与![]() 轴垂直,
轴垂直,![]() 是椭圆
是椭圆![]() 上位于直线
上位于直线![]() 两侧的动点,且满足
两侧的动点,且满足![]() ,试问直线
,试问直线![]() 的斜率是否为定值,请说明理由.
的斜率是否为定值,请说明理由.
参考答案:
【答案】(I)![]() ;(II)为定值
;(II)为定值![]() .
.
【解析】试题分析:
(1)利用题意求得![]() ,则椭圆
,则椭圆![]() 的方程为
的方程为![]() .
.
(2)设出直线的 斜率,联立直线与椭圆的方程可得直线![]() 的斜率为定值
的斜率为定值![]() .
.
试题解析:
解法一:(Ⅰ)因为![]() 的面积是
的面积是![]() 的面积的3倍,
的面积的3倍,
所以![]() ,即
,即![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
则椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)当![]() ,则
,则![]() ,
,
设直线![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() 的斜率为
的斜率为![]() ,
,
不妨设点![]() 在
在![]() 轴上方,
轴上方,![]() ,设
,设![]() ,
,
则![]() 的直线方程为
的直线方程为![]() ,代入
,代入![]() 中整理得
中整理得
![]()
![]() ,
,
![]() ;
;
同理![]() .
.
所以![]() ,
,![]() ,
,
则![]() ,
,
因此直线![]() 的斜率是定值
的斜率是定值![]() .
.
解法二:(Ⅰ)同解法一.
(Ⅱ)依题意知直线![]() 的斜率存在,所以设
的斜率存在,所以设![]() 方程:
方程:![]() 代入
代入![]() 中整理得
中整理得
![]() ,设
,设![]() ,
,
所以![]() ,
,![]() ,
,
![]()
![]()
当![]() ,则
,则![]() ,不妨设点
,不妨设点![]() 在
在![]() 轴上方,
轴上方,![]() ,
,
所以![]() ,整理得
,整理得![]() ,
,
所以![]()
![]() ,
,
整理得![]() ,
,
即![]() ,所以
,所以![]() 或
或![]() .
.
当![]() 时,直线
时,直线![]() 过定点
过定点![]() ,不合题意;
,不合题意;
当![]() 时,
时,![]() ,符合题意,
,符合题意,
所以直线![]() 的斜率是定值
的斜率是定值![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修
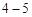 :不等式选讲
:不等式选讲已知函数f(x)=|2x+3|+|2x﹣1|.
(Ⅰ)求不等式f(x)<8的解集;
(Ⅱ)若关于x的不等式f(x)≤|3m+1|有解,求实数m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修
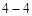 :坐标系与参数方程
:坐标系与参数方程已知曲线C的极坐标方程为ρ﹣4cosθ+3ρsin2θ=0,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l过点M(1,0),倾斜角为
 .
.(Ⅰ)求曲线C的直角坐标方程与直线l的参数方程;
(Ⅱ)若曲线C经过伸缩变换
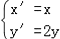 后得到曲线C′,且直线l与曲线C′交于A,B两点,求|MA|+|MB|.
后得到曲线C′,且直线l与曲线C′交于A,B两点,求|MA|+|MB|. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=60°。
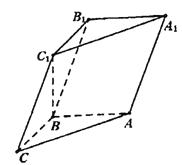
(Ⅰ)求证:C1B⊥平面ABC;
(Ⅱ)设
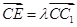 (0≤λ≤1),且平面AB1E与BB1E所成的锐二面角的大小为30°,试求λ的值.
(0≤λ≤1),且平面AB1E与BB1E所成的锐二面角的大小为30°,试求λ的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
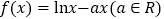 .
.(Ⅰ)讨论函数
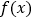 的单调性;
的单调性;(Ⅱ)记函数
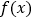 的两个零点分别为
的两个零点分别为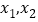 ,且
,且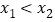 .已知
.已知 ,若不等式
,若不等式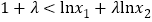 恒成立,求
恒成立,求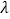 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】集合A是由且备下列性质的函数
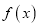 组成的:
组成的:①函数
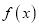 的定义域是
的定义域是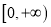 ;②函数
;②函数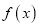 的值域是
的值域是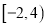 ;
;③函数
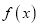 在
在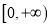 上是增函数,试分别探究下列两小题:
上是增函数,试分别探究下列两小题:(1)判断函数数
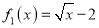 及
及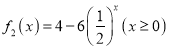 是否属于集合A?并简要说明理由;
是否属于集合A?并简要说明理由;(2)对于(1)中你认为属于集合A的函数
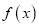 ,不等式
,不等式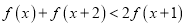
是否对于任意的
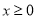 恒成立?若成立,请给出证明;若不成立,请说明理由。
恒成立?若成立,请给出证明;若不成立,请说明理由。 -
科目: 来源: 题型:
查看答案和解析>>【题目】小明同学在寒假社会实践活动中,对白天平均气温与某家奶茶店的
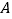 品牌饮料销量之间的关系进行了分析研究,他分别记录了1月11日至1月15日的白天气温
品牌饮料销量之间的关系进行了分析研究,他分别记录了1月11日至1月15日的白天气温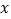 (
(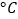 )与该奶茶店的
)与该奶茶店的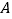 品牌饮料销量
品牌饮料销量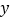 (杯),得到如表数据:
(杯),得到如表数据:日期
1月11号
1月12号
1月13号
1月14号
1月15号
平均气温
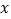 (
(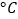 )
)9
10
12
11
8
销量
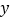 (杯)
(杯)23
25
30
26
21
(1)若先从这五组数据中抽出2组,求抽出的2组数据恰好是相邻2天数据的概率;
(2)请根据所给五组数据,求出
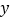 关于
关于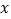 的线性回归方程式
的线性回归方程式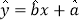 ;
;(3)根据(2)所得的线性回归方程,若天气预报1月16号的白天平均气温为
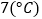 ,请预测该奶茶店这种饮料的销量.
,请预测该奶茶店这种饮料的销量.(参考公式:
 ,
,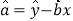 )
)
相关试题

