【题目】已知![]() 中,A(1, 3),AB、AC边上的中线所在直线方程分别为
中,A(1, 3),AB、AC边上的中线所在直线方程分别为![]() 和
和![]() ,求
,求![]() 各边所在直线方程.
各边所在直线方程.
参考答案:
【答案】AB:2y+x-7=0 AC:x-y+2=0 BC:4y-x+1=0
【解析】
试题分析:B点应满足的两个条件是:①B在直线y-1=0上;②BA的中点D在直线x-2y+1=0上.由①可设B(xB,1),进而由②确定xB值,得到B点坐标;同理设出点C的纵坐标,根据中点坐标公式和C在x-2y+1=0上可求出C点坐标,然后利用两点式分别求出三边所在的直线方程即可
试题解析:设B(xB,1)则AB的中点D(![]() ,2)
,2)
∵D在中线CD:x-2y+1=0上
∴![]() 22+1=0,
22+1=0,
解得xB=5,故B(5,1).
同样,因点C在直线x-2y+1=0上,可以设C为(2yC-1,yC),
根据![]() =1,解出yC=-1,
=1,解出yC=-1,
所以C(-3,-1).
根据两点式,得直线AB的方程为y-3= ![]() (x-1);
(x-1);
直线BC的方程为y-1= ![]() (x-5);
(x-5);
直线AC的方程为y-3= ![]() (x-1)
(x-1)
化简得△ABC中直线AB:x+2y-7=0,
直线BC:x-4y-1=0,
直线AC:x-y+2=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场预计全年分批购入每台2000元的电视机共3600台.每批都购入
 台(
台( 是自然数)且每批均需付运费400元.贮存购入的电视机全年所需付的保管费 与每批购入电视机的总价值(不含运费)成正比.若每批购入400台,则全年需用去运输和保管总费用43600元.现在全年只有24000元资金可以支付这笔费用,请问,能否恰当安排每批进货数量,使资金够用?写出你的结论,并说明理由.
是自然数)且每批均需付运费400元.贮存购入的电视机全年所需付的保管费 与每批购入电视机的总价值(不含运费)成正比.若每批购入400台,则全年需用去运输和保管总费用43600元.现在全年只有24000元资金可以支付这笔费用,请问,能否恰当安排每批进货数量,使资金够用?写出你的结论,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
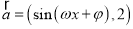 ,
, 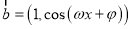 ,
, 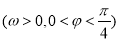 ,函数
,函数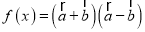 ,已知
,已知 的图像的一个对称中心与它相邻的一条对称轴之间的距离为1,且经过点
的图像的一个对称中心与它相邻的一条对称轴之间的距离为1,且经过点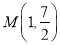
(Ⅰ)求函数
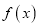 的解析式
的解析式(Ⅱ)先将函数
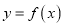 图像上各点的横坐标变为原来的
图像上各点的横坐标变为原来的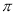 倍,纵坐标不变,再向右平移
倍,纵坐标不变,再向右平移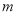
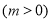 个单位长度,向下平移3个单位长度,得到函数
个单位长度,向下平移3个单位长度,得到函数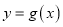 的图像,若函数
的图像,若函数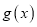 的图像关于原点对称,求实数
的图像关于原点对称,求实数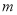 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 .
.(Ⅰ)讨论
 的单调性;
的单调性;(Ⅱ)当
 时,记
时,记 ,已知
,已知 有三个极值点,求
有三个极值点,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司生产一批
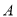 产品需要原材料500吨,每吨原材料可创造利润12万元,该公司通过设备升级,生产这批
产品需要原材料500吨,每吨原材料可创造利润12万元,该公司通过设备升级,生产这批 产品所需原材料减少了
产品所需原材料减少了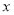 吨,且每吨原材料创造的利润提高了
吨,且每吨原材料创造的利润提高了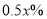 ;若将少用的
;若将少用的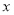 吨原材料全部用于生产公司新开发的
吨原材料全部用于生产公司新开发的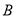 产品,每吨原材料创造的利润为
产品,每吨原材料创造的利润为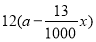 万元,其中
万元,其中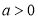 .
.(1)若设备升级后生产这批
 产品的利润不低于原来生产该批
产品的利润不低于原来生产该批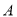 产品的利润,求
产品的利润,求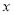 的取值范围;
的取值范围;(2)若生产这批
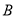 产品的利润始终不高于设备升级后生产这批
产品的利润始终不高于设备升级后生产这批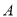 产品的利润,求
产品的利润,求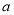 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了弘扬民族文化,某校举行了“我爱国学,传诵经典”考试,并从中随机抽取了100名考生的成绩(得分均为整数,满分100分)进行统计制表,其中成绩不低于80分的考生被评为优秀生,请根据频率分布表中所提供的数据,用频率估计概率,回答下列问题.
分组
频数
频率

5

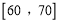
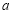
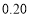
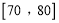
35
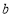
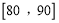
25
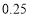
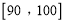
15
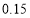
合计
100
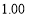
(Ⅰ)求
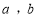 的值及随机抽取一考生恰为优秀生的概率;
的值及随机抽取一考生恰为优秀生的概率;(Ⅱ)按成绩采用分层抽样抽取20人参加学校的“我爱国学”宣传活动,求其中优秀生的人数;
(Ⅲ)在第(Ⅱ)问抽取的优秀生中指派2名学生担任负责人,求至少一人的成绩在
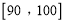 的概率.
的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
 ,底面
,底面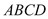 为直角梯形,
为直角梯形,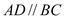 ,
,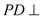 底面
底面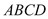 ,
,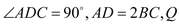 为
为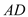 的中点,
的中点,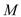 为棱
为棱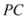 的中点.
的中点.(Ⅰ)证明:
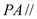 平面
平面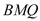 ;
;(Ⅱ)已知
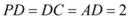 ,求点
,求点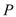 到平面
到平面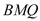 的距离.
的距离.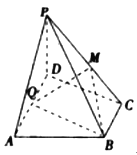
相关试题

