【题目】
11分制乒乓球比赛,每赢一球得1分,当某局打成10:10平后,每球交换发球权,先多得2分的一方获胜,该局比赛结束.甲、乙两位同学进行单打比赛,假设甲发球时甲得分的概率为0.5,乙发球时甲得分的概率为0.4,各球的结果相互独立.在某局双方10:10平后,甲先发球,两人又打了X个球该局比赛结束.
(1)求P(X=2);
(2)求事件“X=4且甲获胜”的概率.
参考答案:
【答案】(1)![]() ;(2)0.1
;(2)0.1
【解析】
(1)本题首先可以通过题意推导出![]() 所包含的事件为“甲连赢两球或乙连赢两球”,然后计算出每种事件的概率并求和即可得出结果;
所包含的事件为“甲连赢两球或乙连赢两球”,然后计算出每种事件的概率并求和即可得出结果;
(2)本题首先可以通过题意推导出![]() 所包含的事件为“前两球甲乙各得
所包含的事件为“前两球甲乙各得![]() 分,后两球均为甲得分”,然后计算出每种事件的概率并求和即可得出结果。
分,后两球均为甲得分”,然后计算出每种事件的概率并求和即可得出结果。
(1)由题意可知,![]() 所包含的事件为“甲连赢两球或乙连赢两球”
所包含的事件为“甲连赢两球或乙连赢两球”
所以![]()
(2)由题意可知,![]() 包含的事件为“前两球甲乙各得
包含的事件为“前两球甲乙各得![]() 分,后两球均为甲得分”
分,后两球均为甲得分”
所以![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC的内角A,B,C所对的边分别为a,b,c.向量
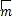 =(a,
=(a,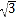 b)与
b)与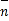 =(cosA,sinB)平行.
=(cosA,sinB)平行.(1)求A;
(2)若a=
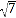 ,b=2,求△ABC的面积.
,b=2,求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直四棱柱ABCD–A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.
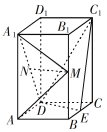
(1)证明:MN∥平面C1DE;
(2)求二面角A-MA1-N的正弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】a,b为空间中两条互相垂直的直线,等腰直角三角形ABC的直角边AC所在直线与a,b都垂直,斜边AB以直线AC为旋转轴旋转,有下列结论:
①当直线AB与a成60°角时,AB与b成30°角;
②当直线AB与a成60°角时,AB与b成60°角;
③直线AB与a所成角的最小值为45°;
④直线AB与a所成角的最大值为60°.
其中正确的是________.(填写所有正确结论的编号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
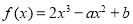 .
.(1)讨论
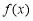 的单调性;
的单调性;(2)是否存在
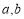 ,使得
,使得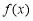 在区间
在区间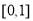 的最小值为
的最小值为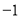 且最大值为1?若存在,求出
且最大值为1?若存在,求出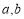 的所有值;若不存在,说明理由.
的所有值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】己知函数
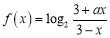 是函数值不恒为零的奇函数,函数
是函数值不恒为零的奇函数,函数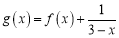 .
.(1)求实数
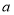 的值,并判断函数
的值,并判断函数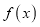 的单调性;
的单调性;(2)解关于
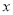 的不等式
的不等式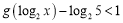 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
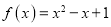 .
.(1)对于实数
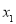 ,
,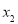 ,若
,若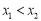 ,有
,有 ,求证:方程
,求证:方程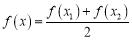 有两个不相等的实数根;
有两个不相等的实数根;(2)若
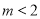 ,函数
,函数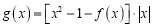 ,求函数
,求函数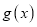 在区间
在区间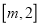 上的最大值和最小值;
上的最大值和最小值;(3)若存在实数
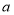 ,使得对于任意实数
,使得对于任意实数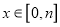 ,都有
,都有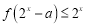 ,求实数
,求实数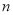 的取值范围.
的取值范围.
相关试题

