【题目】如图,在四棱锥P﹣ABCD中,AB⊥平面BCP,CD∥平面ABP,AB=BC=CP=BP=2CD=2 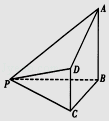
(1)证明:平面ABP⊥平面ADP;
(2)若直线PA与平面PCD所成角为α,求sinα的值.
参考答案:
【答案】
(1)证明:取AP的中点E,PB的中点F,连结DE,EF,CF,
则EF ![]() AB,
AB,
∵CD∥平面ABP,CD平面ABCD,平面ABCD∩平面ABP=AB,
∴CD∥AB,又CD= ![]() AB,
AB,
∴EF ![]() CD,
CD,
∴四边形DEFC是平行四边形,∴CF∥DE,
∵AB⊥平面BCP,CF平面BCP,
∴AB⊥CF,
∵BC=CP=BP,
∴CF⊥PB,又PB∩AB=B,
∴CF⊥平面ABP,
∴DE⊥平面ABP,又DE平面ADP,
∴平面ABP⊥平面ADP.
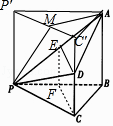
(2))解:过P作PP′∥AB,使得PP′=2,延长CD到C′,使得CC′=2,连结AC′,AP′,C′P′,
则直三棱柱PBC﹣P′AC′所有棱长均为2,
取P′C′的中点M,连结AM,则AM⊥平面PCC′P′,
∴∠APM是直线AP与平面PCD所成的角,即∠APM=α,
∵AM= ![]() =
= ![]() ,PA=
,PA= ![]() =2
=2 ![]() ,
,
∴sinα=sin∠APM= ![]() =
= ![]() =
= ![]() .
.
【解析】(1)取AP的中点E,PB的中点F,连结DE,EF,CF,利用平行四边形得出DE∥CF,通过证明CF⊥平面APB得出DE⊥平面PAB,于是平面ABP⊥平面ADP;(2)将几何体补成直三棱柱,作出线面角,从而可求出sinα的值.
【考点精析】解答此题的关键在于理解平面与平面垂直的判定的相关知识,掌握一个平面过另一个平面的垂线,则这两个平面垂直,以及对空间角的异面直线所成的角的理解,了解已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则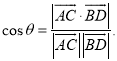 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某圆拱桥的圆拱跨度为20 m,拱高为4 m.现有一船,宽10 m,水面以上高3 m,这条船能否从桥下通过?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l经过抛物线y2=6x的焦点F,且与抛物线相交于A,B两点.
(1)若直线l的倾斜角为60°,求|AB|的值;
(2)若|AB|=9,求线段AB的中点M到准线的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两人玩猜数字游戏,先由甲心中任想一个数字记为
 ,再由乙猜甲刚才想的数字,把乙猜的数字记为
,再由乙猜甲刚才想的数字,把乙猜的数字记为 ,且
,且 、
、 .若
.若 ,则称甲乙“心有灵犀”.现任意找两人玩这个游戏,则二人“心有灵犀”的概率为__________.
,则称甲乙“心有灵犀”.现任意找两人玩这个游戏,则二人“心有灵犀”的概率为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,角
,角 的终边经过点
的终边经过点 .若
.若 是
是 的图象上任意两点,且当
的图象上任意两点,且当 时,
时, 的最小值为
的最小值为 .
.(1)求
 或
或 的值;
的值;(2)求函数
 在
在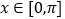 上的单调递减区间;
上的单调递减区间;(3)当
 时,不等式
时,不等式 恒成立,求
恒成立,求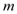 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校乒乓球队有3名男同学A,B,C和3名女同学X,Y,Z,其年级情况如下表:
一年级
二年级
三年级
男同学
A
B
C
女同学
X
Y
Z
现从这6名同学中随机选出2人参加乒乓球比赛(每人被选到的可能性相同).
(1)用表中字母列举出所有可能的结果;
(2)设M为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件M发生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某射击运动员,每次击中目标的概率都是0.8.现采用随机模拟的方法估计该运动员射击4次至少击中3次的概率:先由计算器算出0到9之间取整数值的随机数,指定0,1表示没有击中目标,2,3,4,5,6,7,8,9表示击中目标;因为射击4次,故以每4个随机数为一组,代表射击4次的结果.经随机模拟产生了如下20组随机数:
5727 0293 7140 9857 0347
4373 8636 9647 1417 4698
0371 6233 2616 8045 6011
3661 9597 7424 6710 4281
据此估计,该射击运动员射击4次至少击中3次的概率为_____.
相关试题

