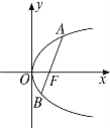
【题目】已知直线l经过抛物线y2=6x的焦点F,且与抛物线相交于A,B两点.
(1)若直线l的倾斜角为60°,求|AB|的值;
(2)若|AB|=9,求线段AB的中点M到准线的距离.
参考答案:
【答案】(1)8(2)![]()
【解析】
(1)由y2=6x,得准线方程、焦点![]() ,直线
,直线![]() 的方程为
的方程为![]() ,与抛物线方程联立可得x2-5x+
,与抛物线方程联立可得x2-5x+![]() =0,设A(x1,y1),B(x2,y2),则x1+x2=5,由抛物线的定义可知线段AB的长;
=0,设A(x1,y1),B(x2,y2),则x1+x2=5,由抛物线的定义可知线段AB的长;
(2)![]() ,即可求线段AB的中点M到准线的距离.
,即可求线段AB的中点M到准线的距离.
(1)因为直线l的倾斜角为60°,所以其斜率k=tan 60°=![]() .
.
又F![]() ,所以直线l的方程为y=
,所以直线l的方程为y=![]()
![]() .
.
联立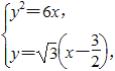 消去y得x2-5x+
消去y得x2-5x+![]() =0.设A(x1,y1),B(x2,y2),则x1+x2=5,
=0.设A(x1,y1),B(x2,y2),则x1+x2=5,
而|AB|=|AF|+|BF|=x1+![]() +x2+
+x2+![]() =x1+x2+p,所以|AB|=5+3=8.
=x1+x2+p,所以|AB|=5+3=8.
(2)设A(x1,y1),B(x2,y2),由抛物线定义知|AB|=|AF|+|BF|=x1+x2+p=x1+x2+3,
所以x1+x2=6,于是线段AB的中点M的横坐标是3.又准线方程是x=-![]() ,
,
所以M到准线的距离为3+![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】传承传统文化再掀热潮,我校举行传统文化知识竞赛.其中两位选手在个人追逐赛中的比赛得分如茎叶图所示,则下列说法正确的是( )

A. 甲的平均数大于乙的平均数
B. 甲的中位数大于乙的中位数
C. 甲的方差大于乙的方差
D. 甲的平均数等于乙的中位数
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列
 和等比数列
和等比数列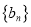 满足
满足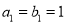 ,
,  ,
,  .
.(1)求
 的通项公式;
的通项公式;(2)求和:
 .
.【答案】(1)
 ;(2)
;(2) .
.【解析】试题分析:(1)根据等差数列
 的
的 ,
,  ,列出关于首项
,列出关于首项 、公差
、公差 的方程组,解方程组可得
的方程组,解方程组可得 与
与 的值,从而可得数列
的值,从而可得数列 的通项公式;(2)利用已知条件根据题意列出关于首项
的通项公式;(2)利用已知条件根据题意列出关于首项 ,公比
,公比 的方程组,解得
的方程组,解得 、
、 的值,求出数列
的值,求出数列 的通项公式,然后利用等比数列求和公式求解即可.
的通项公式,然后利用等比数列求和公式求解即可.试题解析:(1)设等差数列{an}的公差为d. 因为a2+a4=10,所以2a1+4d=10.解得d=2.
所以an=2n1.
(2)设等比数列的公比为q. 因为b2b4=a5,所以b1qb1q3=9.
解得q2=3.所以
 .
.从而
 .
.【题型】解答题
【结束】
18【题目】已知命题
 :实数
:实数 满足
满足 ,其中
,其中 ;命题
;命题 :方程
:方程 表示双曲线.
表示双曲线.(1)若
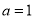 ,且
,且 为真,求实数
为真,求实数 的取值范围;
的取值范围;(2)若
 是
是 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某圆拱桥的圆拱跨度为20 m,拱高为4 m.现有一船,宽10 m,水面以上高3 m,这条船能否从桥下通过?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两人玩猜数字游戏,先由甲心中任想一个数字记为
 ,再由乙猜甲刚才想的数字,把乙猜的数字记为
,再由乙猜甲刚才想的数字,把乙猜的数字记为 ,且
,且 、
、 .若
.若 ,则称甲乙“心有灵犀”.现任意找两人玩这个游戏,则二人“心有灵犀”的概率为__________.
,则称甲乙“心有灵犀”.现任意找两人玩这个游戏,则二人“心有灵犀”的概率为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,AB⊥平面BCP,CD∥平面ABP,AB=BC=CP=BP=2CD=2
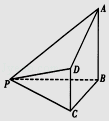
(1)证明:平面ABP⊥平面ADP;
(2)若直线PA与平面PCD所成角为α,求sinα的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,角
,角 的终边经过点
的终边经过点 .若
.若 是
是 的图象上任意两点,且当
的图象上任意两点,且当 时,
时, 的最小值为
的最小值为 .
.(1)求
 或
或 的值;
的值;(2)求函数
 在
在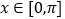 上的单调递减区间;
上的单调递减区间;(3)当
 时,不等式
时,不等式 恒成立,求
恒成立,求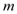 的最大值.
的最大值.
相关试题

