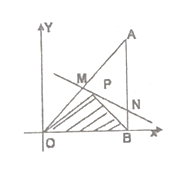
【题目】如图所示,将一块直角三角形木板![]() 置于平面直角坐标系中,已知
置于平面直角坐标系中,已知![]() ,点
,点![]() 是三角形木板内一点,现因三角形木板中阴影部分受到损坏,要把损坏部分锯掉,可用经过点
是三角形木板内一点,现因三角形木板中阴影部分受到损坏,要把损坏部分锯掉,可用经过点![]() 的任一直线
的任一直线![]() 将三角形木板锯成
将三角形木板锯成![]() .设直线
.设直线![]() 的斜率为
的斜率为![]() .
.
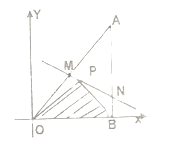
(Ⅰ)求点![]() 的坐标及直线
的坐标及直线![]() 的斜率
的斜率![]() 的范围;
的范围;
(Ⅱ)令![]() 的面积为
的面积为![]() ,试求出
,试求出![]() 的取值范围;
的取值范围;
(Ⅲ)令(Ⅱ)中![]() 的取值范围为集合
的取值范围为集合![]() ,若
,若![]() 对
对![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(Ⅰ) 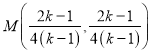 ;
; ![]() ;
; ![]() .(Ⅱ)
.(Ⅱ) ![]() ;(Ⅲ)
;(Ⅲ) ![]() .
.
【解析】试题分析:(Ⅰ)由已知可得:直线![]() 方程为:
方程为: ![]() 直线
直线![]() 方程为:
方程为: ![]() ,分别与直线
,分别与直线![]() 的方程联立即可得出点
的方程联立即可得出点![]() 的坐标;由
的坐标;由![]() 在坐标系中的位置可求斜率
在坐标系中的位置可求斜率
![]() 的取值范围
的取值范围
(Ⅱ)利用三角形的面积计算公式可得![]() ,通过换元利用导数即可得出其单调性最值,进而得出
,通过换元利用导数即可得出其单调性最值,进而得出![]() 的取值范围区间D;
的取值范围区间D;
(Ⅲ)已知![]() 对任意
对任意![]() 恒成立.可转化为
恒成立.可转化为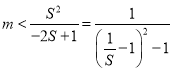
![]() 再利用二次函数的单调性即可得出.
再利用二次函数的单调性即可得出.
试题解析:((Ⅰ)∵![]() ,
,
∴直线![]() 方程为:
方程为: ![]()
直线![]() 方程为:
方程为: ![]() ,
,
由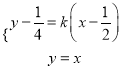 得
得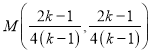 .
.
∵![]() ,∴
,∴![]() 或
或![]() ,
,
又由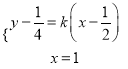 得
得![]() 且
且![]() ,
,
得![]() ,∴
,∴![]() .
.
(Ⅱ)![]()
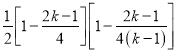
![]() .
.
设![]() ,
, ![]() .
.
∵![]() 在
在![]() 是单调递增.∴当
是单调递增.∴当![]() 时,
时, ![]() ,即当
,即当![]() 时即
时即![]() 时,
时, ![]() ,
, ![]() ,∴
,∴![]() .
.
(Ⅲ)已知![]() 对任意
对任意![]() 恒成立.
恒成立.
又∵![]() ,∴
,∴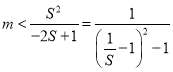 ,
,
![]() .∴
.∴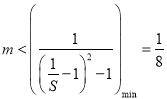 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和为Sn , 若4Sn=(2n﹣1)an+1+1,且a1=1.
(1)求数列{an}的通项公式;
(2)设cn=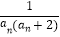 ,数列{cn}的前n项和为Tn .
,数列{cn}的前n项和为Tn .
①求Tn;
②对于任意的n∈N*及x∈R,不等式kx2﹣6kx+k+7+3Tn>0恒成立,求实数k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】 用总长14.8米的钢条制作一个长方体容器的框架,如果所制容器底面一边的长比另一边的长多0.5米,那么高为多少时容器的容积最大?最大容积是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
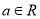 ,若
,若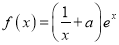 在区间
在区间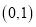 上有且只有一个极值点,则
上有且只有一个极值点,则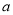 的取值范围是( )
的取值范围是( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列{an}中,a1=1,a3=﹣3.
(1)求数列{an}的通项公式;
(2)若数列{an}的前k项和Sk=﹣35,求k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A、B、C为△ABC的三个内角,且其对边分别为a、b、c,若cosBcosC﹣sinBsinC=
 .
.
(1)求角A;
(2)若a=2 ,b+c=4,求△ABC的面积.
,b+c=4,求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2+ax+6.
(1)当a=5时,解不等式f(x)<0;
(2)若不等式f(x)>0的解集为R,求实数a的取值范围.
相关试题

