【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π,x∈R)在一个周期内的图象如图所示,则函数的解析式为 . 直线y= ![]() 与函数y=f(x)(x∈R)图象的所有交点的坐标为 .
与函数y=f(x)(x∈R)图象的所有交点的坐标为 . 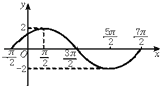
参考答案:
【答案】f(x)=2sin( ![]() x+
x+ ![]() );(
);( ![]() +4kπ,
+4kπ, ![]() )或(
)或( ![]() +4kπ,
+4kπ, ![]() )(k∈Z)
)(k∈Z)
【解析】解:∵f(x)=Asin(ωx+φ)(A>0,ω>0,x∈R),
∴A=2,周期T= ![]() =
= ![]() ﹣(﹣
﹣(﹣ ![]() )=4π,
)=4π,
∴ω= ![]() .
.
∴f(x)=2sin( ![]() x+φ),
x+φ),
又f(﹣ ![]() )=2sin(
)=2sin( ![]() ×(﹣
×(﹣ ![]() )+φ)=0,
)+φ)=0,
∴φ﹣ ![]() =kπ,k∈Z,|φ|<π,
=kπ,k∈Z,|φ|<π,
∴φ= ![]() .
.
∴f(x)=2sin( ![]() x+
x+ ![]() ).
).
当f(x)= ![]() 时,即2sin(
时,即2sin( ![]() x+
x+ ![]() )=
)= ![]() ,可得sin(
,可得sin( ![]() x+
x+ ![]() )=
)= ![]() ,
,
∴ ![]() x+
x+ ![]() =
= ![]() +2kπ或
+2kπ或 ![]() x+
x+ ![]() =
= ![]() +2kπ(k∈Z),可得x=
+2kπ(k∈Z),可得x= ![]() +4kπ或
+4kπ或 ![]() +4kπ(k∈Z)
+4kπ(k∈Z)
由此可得,直线y= ![]() 与函数f(x)图象的所有交点的坐标为:(
与函数f(x)图象的所有交点的坐标为:( ![]() +4kπ,
+4kπ, ![]() )或(
)或( ![]() +4kπ,
+4kπ, ![]() )(k∈Z).
)(k∈Z).
所以答案是:f(x)=2sin( ![]() x+
x+ ![]() ),(
),( ![]() +4kπ,
+4kπ, ![]() )或(
)或( ![]() +4kπ,
+4kπ, ![]() )(k∈Z).
)(k∈Z).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
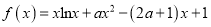 ,其中
,其中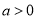 .
.(1)求函数
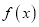 的单调区间;
的单调区间;(2)对任意
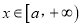 ,都有
,都有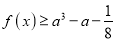 ,求实数
,求实数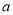 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆E:
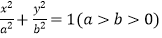 的右焦点为F(3,0),过点F的直线交椭圆E于A、B两点.若AB的中点坐标为(1,﹣1),则E的方程为( )
的右焦点为F(3,0),过点F的直线交椭圆E于A、B两点.若AB的中点坐标为(1,﹣1),则E的方程为( )
A.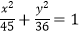
B.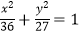
C.
D.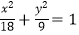
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C:(x﹣1)2+(y﹣2)2=25及直线l:(2m+1)x+(m+1)y=7m+4.(m∈R)
(1)证明:不论m取什么实数,直线l与圆C恒相交;
(2)求直线l与圆C所截得的弦长的最短长度及此时直线l的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知cosx=﹣
 ,x∈(0,π)
,x∈(0,π)
(1)求cos(x﹣ )的值;
)的值;
(2)求sin(2x+ )的值.
)的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
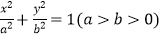 ,点P(
,点P( 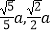 )在椭圆上.
)在椭圆上.
(1)求椭圆的离心率;
(2)设A为椭圆的左顶点,O为坐标原点.若点Q在椭圆上且满足|AQ|=|AO|,求直线OQ的斜率的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某厂家为了了解某新产品使用者的年龄情况,现随机调査100 位使用者的年龄整理后画出的频率分布直方图如图所示.

(1)求100名使用者中各年龄组的人数,并利用所给的频率分布直方图估计所有使用者的平均年龄;
(2)若已从年龄在
 的使用者中利用分层抽样选取了6人,再从这6人中选出2人,求这2人在不同的年龄组的概率.
的使用者中利用分层抽样选取了6人,再从这6人中选出2人,求这2人在不同的年龄组的概率.
相关试题

