【题目】已知椭圆 ![]() ,点P(
,点P( ![]() )在椭圆上.
)在椭圆上.
(1)求椭圆的离心率;
(2)设A为椭圆的左顶点,O为坐标原点.若点Q在椭圆上且满足|AQ|=|AO|,求直线OQ的斜率的值.
参考答案:
【答案】
(1)解:因为点P( ![]() )在椭圆上,所以
)在椭圆上,所以 ![]()
∴ ![]()
∴ ![]()
∴ ![]()
(2)解:设直线OQ的斜率为,则其方程为y=kx
设点Q的坐标为(x0,y0),由条件得 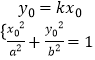 ,消元并整理可得
,消元并整理可得 ![]() ①
①
∵|AQ|=|AO|,A(﹣a,0),y0=kx0,
∴ ![]()
∴ ![]()
∵x0≠0,∴ ![]()
代入①,整理得 ![]()
∵ ![]()
∴ ![]() +4,
+4,
∴5k4﹣22k2﹣15=0
∴k2=5
∴ ![]()
【解析】(1)根据点P( ![]() )在椭圆上,可得
)在椭圆上,可得 ![]() ,由此可求椭圆的离心率;(2)设直线OQ的斜率为k,则其方程为y=kx,设点Q的坐标为(x0 , y0),与椭圆方程联立,
,由此可求椭圆的离心率;(2)设直线OQ的斜率为k,则其方程为y=kx,设点Q的坐标为(x0 , y0),与椭圆方程联立, ![]() ,根据|AQ|=|AO|,A(﹣a,0),y0=kx0 , 可求
,根据|AQ|=|AO|,A(﹣a,0),y0=kx0 , 可求 ![]() ,由此可求直线OQ的斜率的值.
,由此可求直线OQ的斜率的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C:(x﹣1)2+(y﹣2)2=25及直线l:(2m+1)x+(m+1)y=7m+4.(m∈R)
(1)证明:不论m取什么实数,直线l与圆C恒相交;
(2)求直线l与圆C所截得的弦长的最短长度及此时直线l的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π,x∈R)在一个周期内的图象如图所示,则函数的解析式为 . 直线y=
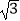 与函数y=f(x)(x∈R)图象的所有交点的坐标为 .
与函数y=f(x)(x∈R)图象的所有交点的坐标为 . 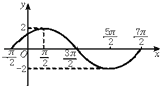
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知cosx=﹣
 ,x∈(0,π)
,x∈(0,π)
(1)求cos(x﹣ )的值;
)的值;
(2)求sin(2x+ )的值.
)的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某厂家为了了解某新产品使用者的年龄情况,现随机调査100 位使用者的年龄整理后画出的频率分布直方图如图所示.

(1)求100名使用者中各年龄组的人数,并利用所给的频率分布直方图估计所有使用者的平均年龄;
(2)若已从年龄在
 的使用者中利用分层抽样选取了6人,再从这6人中选出2人,求这2人在不同的年龄组的概率.
的使用者中利用分层抽样选取了6人,再从这6人中选出2人,求这2人在不同的年龄组的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2sinx(sinx+
 cosx)﹣1(其中x∈R),求:
cosx)﹣1(其中x∈R),求:
(1)函数f(x)的最小正周期;
(2)函数f(x)的单调减区间;
(3)函数f(x)图象的对称轴和对称中心. -
科目: 来源: 题型:
查看答案和解析>>【题目】设△ABC的内角A,B,C所对的边分别为a,b,c,已知a=2,b=3,cosC=
 .
.
(1)求△ABC的面积;
(2)求sin(C﹣A)的值.
相关试题

