【题目】已知函数![]() ,其中
,其中![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)对任意![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)函数的定义域为![]() (2)
(2)![]() 的取值范围是
的取值范围是![]()
【解析】试题分析:(1)求函数的导数,利用函数单调性和导数之间的关系,即可求解函数的单调区间;
(2)对于任意![]() ,都有
,都有![]() ,转化为
,转化为![]() ,多次构造函数,求函数的导数,利用导数研究函数的最值可求函数求实数
,多次构造函数,求函数的导数,利用导数研究函数的最值可求函数求实数![]() 的取值范围.
的取值范围.
试题解析:(1)函数的定义域为![]() ,
,
函数的导数![]() ,
,
因为![]() ,
,
所以当![]() 时,
时, ![]() ,此时
,此时![]() ,函数
,函数![]() 在
在![]() 上单调递减,
上单调递减,
当![]() 时,
时, ![]() ,此时
,此时![]() ,函数
,函数![]() 在
在![]() 上单调递增,
上单调递增,
所以函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(2)当![]() 时,由(1)知
时,由(1)知![]() 在
在![]() 上单调递减,
上单调递减, ![]() 在
在![]() 上单调递减,
上单调递减,
所以对任意的![]() ,都有
,都有![]() ,
,
因为对任意的![]() ,都有
,都有![]() ,
,
所以![]() ,即
,即![]() ,得
,得![]() ,
,
所以当![]() 时,对于任意的
时,对于任意的![]() ,都有
,都有![]() ,
,
当![]() 时,
时, ![]() ,由(1)得
,由(1)得![]() 在
在![]() 上单调递增,
上单调递增,
所以对于任意![]() ,有
,有![]() ,
,
因为对于任意![]() ,都有
,都有![]() ,
,
所以![]() ,即
,即![]() ,
,
设![]() ,则
,则![]() ,
,
设![]() ,
,
则![]() ,所以
,所以![]() 在
在![]() 上单调递减,
上单调递减,
则当![]() 时,
时, ![]() ,
,
此时不等式![]() 不成立,
不成立,
综上,所求![]() 的取值范围是
的取值范围是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面给出的关系式中正确的个数是( )
①
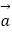 =
= 
②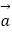
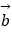 =
= 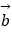
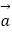
③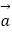 2=|
2=| 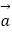 |2
|2
④(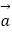
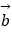 )
) 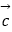 =
= 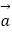 (
( 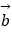
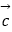 )
)
⑤|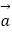
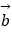 |≤
|≤ 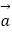
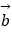 .
.
A.0
B.1
C.2
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数

(1)若
 ,求函数
,求函数 的极值;
的极值;(2)若
 ,
,  ,
,  ,使得
,使得 (
( ),求实数
),求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义平面向量之间的一种运算“⊙”如下:对任意的
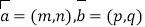 ,令
,令 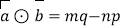 ,下面说法错误的是( )
,下面说法错误的是( )
A.若 与
与 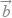 共线,则
共线,则  ⊙
⊙ 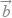 =0
=0
B. ⊙
⊙ 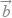 =
= 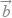 ⊙
⊙ 
C.对任意的λ∈R,有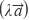 ⊙
⊙ 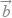 =
= 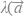 ⊙
⊙ 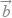 )
)
D.( ⊙
⊙ 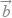 )2+(
)2+(  )2=|
)2=|  |2|
|2| 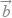 |2
|2 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆E:
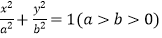 的右焦点为F(3,0),过点F的直线交椭圆E于A、B两点.若AB的中点坐标为(1,﹣1),则E的方程为( )
的右焦点为F(3,0),过点F的直线交椭圆E于A、B两点.若AB的中点坐标为(1,﹣1),则E的方程为( )
A.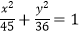
B.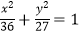
C.
D.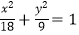
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C:(x﹣1)2+(y﹣2)2=25及直线l:(2m+1)x+(m+1)y=7m+4.(m∈R)
(1)证明:不论m取什么实数,直线l与圆C恒相交;
(2)求直线l与圆C所截得的弦长的最短长度及此时直线l的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π,x∈R)在一个周期内的图象如图所示,则函数的解析式为 . 直线y=
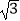 与函数y=f(x)(x∈R)图象的所有交点的坐标为 .
与函数y=f(x)(x∈R)图象的所有交点的坐标为 . 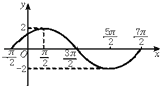
相关试题

