【题目】某工厂修建一个长方体无盖蓄水池,其容积为4 800立方米,深度为3米.池底每平方米的造价为150元,池壁每平方米的造价为120元.设池底长方形长为x米.
(1)求底面积,并用含x的表达式表示池壁面积;
(2)怎样设计水池能使总造价最低?最低造价是多少?
参考答案:
【答案】(1)1600,![]() (平方米);(2)池底设计为边长40米的正方形时总造价最低,最低造价为268800元.
(平方米);(2)池底设计为边长40米的正方形时总造价最低,最低造价为268800元.
【解析】
(1)根据题意,由于修建一个长方体无盖蓄水池,
其容积为4 800立方米,深度为3米.
可得底面积为1600,池壁面积s=![]() .
.
(2)同时池底每平方米的造价为150元,池壁每平方米的造价为120元.
设池底长方形长为x米,
则可知总造价s=![]() ,x=40时,
,x=40时,
则![]() .
.
故可知当x=40时,则有可使得总造价最低,
最低造价是268800元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,其中
,其中 且
且 ,设
,设 .
.(Ⅰ)求函数
 的定义域,判断
的定义域,判断 的奇偶性,并说明理由;
的奇偶性,并说明理由;(Ⅱ)若
 ,求使
,求使 成立的
成立的 的集合.
的集合. -
科目: 来源: 题型:
查看答案和解析>>【题目】数列{an}满足an+1+(﹣1)nan=2n﹣1,则{an}的前60项和为( )
A. 3690 B. 3660 C. 1845 D. 1830
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小组为了研究昼夜温差对一种稻谷种子发芽情况的影响,他们分别记录了4月1日至4月5日的每天星夜温差与实验室每天每100颗种子的发芽数,得到如下资料:
日期
4月1日
4月2日
4月3日
4月4日
4月5日
温差

9
10
11
8
12
发芽数
 (颗)
(颗)38
30
24
41
17
利用散点图,可知
 线性相关。
线性相关。(1)求出
 关于
关于 的线性回归方程,若4月6日星夜温差
的线性回归方程,若4月6日星夜温差 ,请根据你求得的线性同归方程预测4月6日这一天实验室每100颗种子中发芽颗数;
,请根据你求得的线性同归方程预测4月6日这一天实验室每100颗种子中发芽颗数;(2)若从4月1日
 4月5日的五组实验数据中选取2组数据,求这两组恰好是不相邻两天数据的概率.
4月5日的五组实验数据中选取2组数据,求这两组恰好是不相邻两天数据的概率.(公式:
 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如果
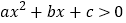 的解集为
的解集为 ,则对于函数
,则对于函数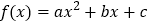 应有
应有 ( )
A.
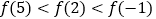 B.
B. 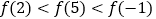
C.
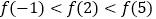 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于的不等式
 的解集为
的解集为 ;
;(1)若
 ,求
,求 的取值范围;
的取值范围;(2)若存在两个不相等负实数
 、
、 ,使得
,使得 ,求实数
,求实数 的取值范围;
的取值范围;(3)是否存在实数
 ,满足:“对于任意
,满足:“对于任意 ,都有
,都有 ,对于任意的
,对于任意的 ,都有
,都有 ”,若存在,求出
”,若存在,求出 的值,若不存在,说明理由.
的值,若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某小组为了研究昼夜温差对一种稻谷种子发芽情况的影响,他们分别记录了4月1日至4月5日的每天星夜温差与实验室每天每100颗种子的发芽数,得到如下资料:
日期
4月1日
4月2日
4月3日
4月4日
4月5日
温差

9
10
11
8
12
发芽数
 (颗)
(颗)38
30
24
41
17
利用散点图,可知
 线性相关。
线性相关。(1)求出
 关于
关于 的线性回归方程,若4月6日星夜温差
的线性回归方程,若4月6日星夜温差 ,请根据你求得的线性同归方程预测4月6日这一天实验室每100颗种子中发芽颗数;
,请根据你求得的线性同归方程预测4月6日这一天实验室每100颗种子中发芽颗数;(2)若从4月1日
 4月5日的五组实验数据中选取2组数据,求这两组恰好是不相邻两天数据的概率.
4月5日的五组实验数据中选取2组数据,求这两组恰好是不相邻两天数据的概率.(公式:
 )
)
相关试题

