【题目】定义在![]() 上的函数
上的函数![]() 满足对任意
满足对任意![]() ,
,![]() ,恒有
,恒有![]() ,且
,且![]() 不恒为0.
不恒为0.
(1)求![]() 和
和![]() 的值;
的值;
(2)试判断![]() 的奇偶性,并加以证明;
的奇偶性,并加以证明;
(3)若![]() ,恒有
,恒有![]() ,求满足不等式
,求满足不等式![]() 的
的![]() 的取值集合.
的取值集合.
参考答案:
【答案】(1) ![]() ,
,![]() ;(2)详见解析;(3)
;(2)详见解析;(3) ![]() .
.
【解析】试题分析:本题为抽象函数问题,解决抽象函数的基本方法有两种:一是赋值法,二是“打回原型”,赋值法是最常用的解题方法,巧妙的赋值可求出函数的特值,本题的第一步就是赋值法,发也可以判断分别给x,y赋值1和![]() 就可求出所求函数值,给y赋值
就可求出所求函数值,给y赋值![]() 可判断函数的奇偶性,利用
可判断函数的奇偶性,利用![]() 可以证明函数的单调性,借助函数的奇偶性和单调性以及特殊点特殊值可以模拟出函数的图象,在此基础上可以解不等式.
可以证明函数的单调性,借助函数的奇偶性和单调性以及特殊点特殊值可以模拟出函数的图象,在此基础上可以解不等式.
试题解析:
(1)令![]() ,得
,得![]() ,∴
,∴![]() ,
,
令![]() ,得
,得![]() ,∴
,∴![]() .
.
(2)令![]() ,由
,由![]() 可得
可得![]() ,
,
∵![]() ,∴
,∴![]() ,
,
又![]() 不恒为0,∴
不恒为0,∴![]() 是偶函数.
是偶函数.
(3)若![]() 时,恒有
时,恒有![]()
![]() ,此时
,此时![]() 为增函数,
为增函数,
由![]() ,得
,得![]() ,
,
由(2)知,![]() ,∴
,∴![]() ,
,
又∵![]() 在
在![]() 上为增函数,∴
上为增函数,∴![]() ,
,
∴![]() .
.
∴![]() 的取值集合是
的取值集合是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为推动乒乓球运动的发展,某乒乓球比赛允许不同协会的运动员组队参加.现有来自甲协会的运动员
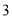 名,其中种子选手
名,其中种子选手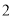 名;乙协会的运动员
名;乙协会的运动员 名,其中种子选手
名,其中种子选手 名.从这
名.从这 名运动员中随机选择
名运动员中随机选择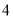 人参加比赛.
人参加比赛.(1)设
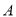 为事件“选出的
为事件“选出的 人中恰有
人中恰有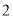 名种子选手,且这
名种子选手,且这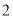 名种子选手来自同一个协会”求事件
名种子选手来自同一个协会”求事件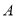 发生的概率;
发生的概率;(2)设
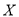 为选出的
为选出的 人中种子选手的人数,求随机变量
人中种子选手的人数,求随机变量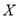 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)是定义在R上且以2为周期的偶函数,当0≤x≤1时,f(x)=x2.如果函数g(x)=f(x)-(x+m)有两个零点,则实数m的值为( )
A.2k(k∈Z) B.2k或2k+
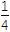 (k∈Z)
(k∈Z)C.0 D.2k或2k-
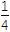 (k∈Z)
(k∈Z) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
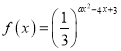 .
.(1)若
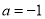 ,求
,求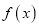 的单调区间;
的单调区间;(2)若
 有最大值
有最大值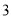 ,求
,求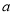 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】若函数f(x)满足f(logax)=
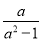 ·(x-
·(x-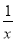 )(其中a>0且a≠1).
)(其中a>0且a≠1).(1)求函数f(x)的解析式,并判断其奇偶性和单调性;
(2)当x∈(-∞,2)时,f(x)-4的值恒为负数,求a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
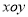 中,
中, 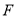 是抛物线
是抛物线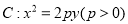 的焦点,
的焦点, 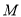 是抛物线
是抛物线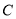 上位于第一象限内的任意一点,过
上位于第一象限内的任意一点,过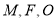 三点的圆的圆心为
三点的圆的圆心为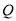 ,点
,点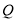 到抛物线
到抛物线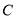 的准线的距离为
的准线的距离为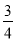
(1)求抛物线
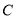 的方程;
的方程;(2)若点
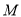 的横坐标为
的横坐标为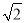 ,直线
,直线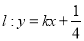 与抛物线
与抛物线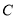 有两个不同的交点
有两个不同的交点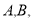
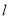 与圆
与圆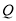 有两个不同的交点
有两个不同的交点 ,求当
,求当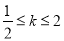 时,
时, 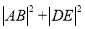 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】2017年1月1日,作为贵阳市打造“千园之城”27个示范性公园之一的泉湖公园正式开园.元旦期间,为了活跃气氛,主办方设置了水上挑战项目向全体市民开放.现从到公园游览的市民中随机抽取了60名男生和40名女生共100人进行调查,统计出100名市民中愿意接受挑战和不愿意接受挑战的男女生比例情况,具体数据如图表:
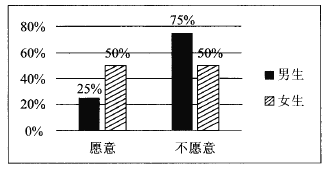
(1)根据条件完成下列
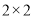 列联表,并判断是否在犯错误的概率不超过1%的情况下愿意接受挑战与性别有关?
列联表,并判断是否在犯错误的概率不超过1%的情况下愿意接受挑战与性别有关?愿意
不愿意
总计
男生
女生
总计
(2)现用分层抽样的方法从愿意接受挑战的市民中选取7名挑战者,再从中抽取2人参加挑战,求抽取的2人中至少有一名男生的概率.
参考数据及公式:
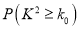
0.1
0.05
0.025
0.01
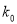
2.706
3.841
5.024
6.635
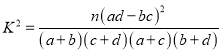 .
.
相关试题

