【题目】若函数f(x)满足f(logax)=![]() ·(x-
·(x-![]() )(其中a>0且a≠1).
)(其中a>0且a≠1).
(1)求函数f(x)的解析式,并判断其奇偶性和单调性;
(2)当x∈(-∞,2)时,f(x)-4的值恒为负数,求a的取值范围.
参考答案:
【答案】(1)见解析.(2)[2-![]() ,1)∪(1,2+
,1)∪(1,2+![]() ].
].
【解析】 试题分析:(1)利用换元法求函数解析式,注意换元时元的范围,再根据奇偶性定义判断函数奇偶性,最后根据复合函数单调性性质判断函数单调性(2)不等式恒成立问题一般转化为对应函数最值问题:即f(x)最大值小于4,根据函数单调性确定函数最大值,自在解不等式可得a的取值范围.
试题解析:
(1)令logax=t(t∈R),则x=at,
∴f(t)=![]() (at-a-t).
(at-a-t).
∴f(x)=![]() (ax-a-x)(x∈R).
(ax-a-x)(x∈R).
∵f(-x)=![]() (a-x-ax)=-
(a-x-ax)=-![]() (ax-a-x)=-f(x),∴f(x)为奇函数.
(ax-a-x)=-f(x),∴f(x)为奇函数.
当a>1时,y=ax为增函数,y=-a-x为增函数,且![]() >0,
>0,
∴f(x)为增函数.
当0<a<1时,y=ax为减函数,y=-a-x为减函数,且![]() <0,
<0,
∴f(x)为增函数.∴f(x)在R上为增函数.
(2)∵f(x)是R上的增函数,∴y=f(x)-4也是R上的增函数.
由x<2,得f(x)<f(2),要使f(x)-4在(-∞,2)上恒为负数,
只需f(2)-4≤0,即![]() (a2-a-2)≤4.
(a2-a-2)≤4.
∴![]() (
(![]() )≤4,∴a2+1≤4a,∴a2-4a+1≤0,
)≤4,∴a2+1≤4a,∴a2-4a+1≤0,
∴2-![]() ≤a≤2+
≤a≤2+![]() .又a≠1,
.又a≠1,
∴a的取值范围为[2-![]() ,1)∪(1,2+
,1)∪(1,2+![]() ].
].
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)是定义在R上且以2为周期的偶函数,当0≤x≤1时,f(x)=x2.如果函数g(x)=f(x)-(x+m)有两个零点,则实数m的值为( )
A.2k(k∈Z) B.2k或2k+
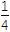 (k∈Z)
(k∈Z)C.0 D.2k或2k-
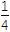 (k∈Z)
(k∈Z) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
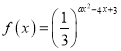 .
.(1)若
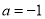 ,求
,求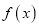 的单调区间;
的单调区间;(2)若
 有最大值
有最大值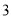 ,求
,求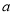 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义在
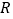 上的函数
上的函数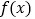 满足对任意
满足对任意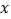 ,
,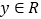 ,恒有
,恒有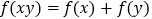 ,且
,且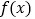 不恒为0.
不恒为0.(1)求
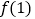 和
和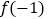 的值;
的值;(2)试判断
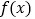 的奇偶性,并加以证明;
的奇偶性,并加以证明;(3)若
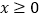 ,恒有
,恒有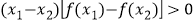 ,求满足不等式
,求满足不等式 的
的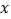 的取值集合.
的取值集合. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
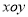 中,
中, 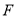 是抛物线
是抛物线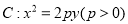 的焦点,
的焦点, 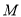 是抛物线
是抛物线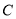 上位于第一象限内的任意一点,过
上位于第一象限内的任意一点,过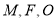 三点的圆的圆心为
三点的圆的圆心为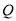 ,点
,点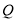 到抛物线
到抛物线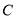 的准线的距离为
的准线的距离为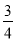
(1)求抛物线
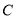 的方程;
的方程;(2)若点
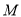 的横坐标为
的横坐标为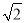 ,直线
,直线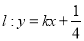 与抛物线
与抛物线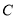 有两个不同的交点
有两个不同的交点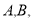
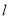 与圆
与圆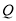 有两个不同的交点
有两个不同的交点 ,求当
,求当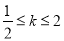 时,
时, 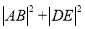 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】2017年1月1日,作为贵阳市打造“千园之城”27个示范性公园之一的泉湖公园正式开园.元旦期间,为了活跃气氛,主办方设置了水上挑战项目向全体市民开放.现从到公园游览的市民中随机抽取了60名男生和40名女生共100人进行调查,统计出100名市民中愿意接受挑战和不愿意接受挑战的男女生比例情况,具体数据如图表:
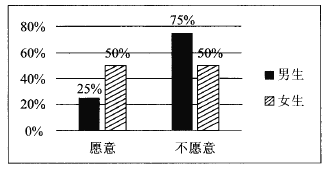
(1)根据条件完成下列
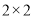 列联表,并判断是否在犯错误的概率不超过1%的情况下愿意接受挑战与性别有关?
列联表,并判断是否在犯错误的概率不超过1%的情况下愿意接受挑战与性别有关?愿意
不愿意
总计
男生
女生
总计
(2)现用分层抽样的方法从愿意接受挑战的市民中选取7名挑战者,再从中抽取2人参加挑战,求抽取的2人中至少有一名男生的概率.
参考数据及公式:
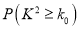
0.1
0.05
0.025
0.01
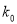
2.706
3.841
5.024
6.635
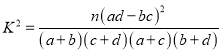 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱柱ABCD-A1B1C1D1中,已知平面AA1C1C⊥平面ABCD,且AB=BC=CA=
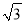 ,AD=CD=1.
,AD=CD=1.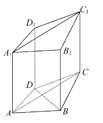
(1)求证:BD⊥AA1.
(2)在棱BC上取一点E,使得AE∥平面DCC1D1,求
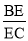 的值.
的值.
相关试题

