【题目】已知函数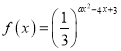 .
.
(1)若![]() ,求
,求![]() 的单调区间;
的单调区间;
(2)若![]() 有最大值
有最大值![]() ,求
,求![]() 的值.
的值.
参考答案:
【答案】(1)递增区间是![]() ,递减区间是
,递减区间是![]() .(2)3
.(2)3
【解析】试题分析:(1)根据复合函数单调性,先根据对称轴求二次函数单调性,再根据复合性研究单调区间(2)根据a讨论,函数单调性,再根据单调性确定函数最大值,最后根据方程解出![]() 的值.
的值.
试题解析:解:(1)当![]() 时,
时, ![]() ,对称轴为
,对称轴为![]() ,所以函数
,所以函数![]() 的递增区间是
的递增区间是![]() ,递减区间是
,递减区间是![]() .
.
(2)当![]() 时,
时, ![]() 单调递增,无最大值
单调递增,无最大值
当![]() 时,
时, ![]() 递增区间是
递增区间是![]() ,递减区间是
,递减区间是![]() ,最大值为
,最大值为![]()
当![]() 时,
时, ![]() 递减区间是
递减区间是![]() ,递增区间是
,递增区间是![]() ,无最大值
,无最大值
综上![]()
点睛:1.复合函数单调性的规则
若两个简单函数的单调性相同,则它们的复合函数为增函数;若两个简单函数的单调性相反,则它们的复合函数为减函数.即“同增异减”.
2.函数单调性的性质
(1)若f(x),g(x)均为区间A上的增(减)函数,则f(x)+g(x)也是区间A上的增(减)函数,更进一步,即增+增=增,增-减=增,减+减=减,减-增=减;
(2)奇函数在其关于原点对称的区间上单调性相同,偶函数在其关于原点对称的区间上单调性相反.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商品的进价为每件
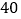 元,售价为每件
元,售价为每件 元,每个月可卖出
元,每个月可卖出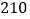 件;如果每件商品在该售价的基础上每上涨
件;如果每件商品在该售价的基础上每上涨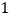 元,则每个月少卖
元,则每个月少卖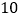 件(每件售价不能高于
件(每件售价不能高于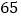 元).设每件商品的售价上涨
元).设每件商品的售价上涨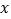 元(
元(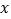 为正整数),每个月的销售利润为
为正整数),每个月的销售利润为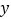 元.
元.(1)求
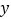 与
与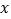 的函数的函数关系式并直接写出自变量
的函数的函数关系式并直接写出自变量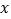 的取值范围;
的取值范围;(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为推动乒乓球运动的发展,某乒乓球比赛允许不同协会的运动员组队参加.现有来自甲协会的运动员
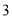 名,其中种子选手
名,其中种子选手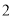 名;乙协会的运动员
名;乙协会的运动员 名,其中种子选手
名,其中种子选手 名.从这
名.从这 名运动员中随机选择
名运动员中随机选择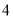 人参加比赛.
人参加比赛.(1)设
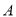 为事件“选出的
为事件“选出的 人中恰有
人中恰有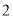 名种子选手,且这
名种子选手,且这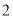 名种子选手来自同一个协会”求事件
名种子选手来自同一个协会”求事件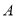 发生的概率;
发生的概率;(2)设
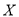 为选出的
为选出的 人中种子选手的人数,求随机变量
人中种子选手的人数,求随机变量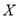 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)是定义在R上且以2为周期的偶函数,当0≤x≤1时,f(x)=x2.如果函数g(x)=f(x)-(x+m)有两个零点,则实数m的值为( )
A.2k(k∈Z) B.2k或2k+
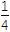 (k∈Z)
(k∈Z)C.0 D.2k或2k-
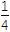 (k∈Z)
(k∈Z) -
科目: 来源: 题型:
查看答案和解析>>【题目】定义在
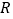 上的函数
上的函数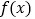 满足对任意
满足对任意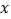 ,
,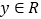 ,恒有
,恒有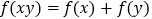 ,且
,且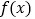 不恒为0.
不恒为0.(1)求
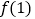 和
和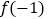 的值;
的值;(2)试判断
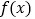 的奇偶性,并加以证明;
的奇偶性,并加以证明;(3)若
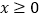 ,恒有
,恒有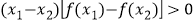 ,求满足不等式
,求满足不等式 的
的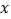 的取值集合.
的取值集合. -
科目: 来源: 题型:
查看答案和解析>>【题目】若函数f(x)满足f(logax)=
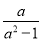 ·(x-
·(x-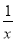 )(其中a>0且a≠1).
)(其中a>0且a≠1).(1)求函数f(x)的解析式,并判断其奇偶性和单调性;
(2)当x∈(-∞,2)时,f(x)-4的值恒为负数,求a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
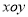 中,
中, 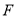 是抛物线
是抛物线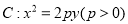 的焦点,
的焦点, 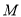 是抛物线
是抛物线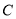 上位于第一象限内的任意一点,过
上位于第一象限内的任意一点,过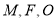 三点的圆的圆心为
三点的圆的圆心为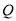 ,点
,点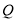 到抛物线
到抛物线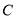 的准线的距离为
的准线的距离为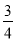
(1)求抛物线
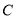 的方程;
的方程;(2)若点
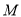 的横坐标为
的横坐标为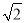 ,直线
,直线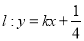 与抛物线
与抛物线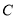 有两个不同的交点
有两个不同的交点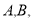
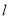 与圆
与圆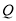 有两个不同的交点
有两个不同的交点 ,求当
,求当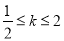 时,
时, 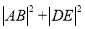 的最小值.
的最小值.
相关试题

