【题目】在2016年6月英国“脱欧”公投前夕,为了统计该国公民是否有“留欧”意愿,该国某中学数学兴趣小组随机抽查了50名不同年龄层次的公民,调查统计他们是赞成“留欧”还是反对“留欧”.现已得知50人中赞成“留欧”的占60%,统计情况如下表:
年龄层次 | 赞成“留欧” | 反对“留欧” | 合计 |
18岁—19岁 | 6 | ||
50岁及50岁以上 | 10 | ||
合计 | 50 |
(1)请补充完整上述列联表;
(2)请问是否有97.5%的把握认为赞成“留欧”与年龄层次有关?请说明理由.
参考公式与数据: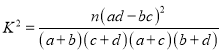 ,其中
,其中![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考答案:
【答案】(1)见解析,(2)有97.5%的把握认为赞成“留欧”与年龄层次有关
【解析】
试题分析:独立性检验的一般步骤(1)根据样本数据制成![]() 列联表,(2)根据公式求出
列联表,(2)根据公式求出![]() 的值,(3)查表比较
的值,(3)查表比较![]() 与临界的大小关系,做出统计判断
与临界的大小关系,做出统计判断
独立性检验是考察两个分类变量是否有关系,计算随机变量的观测值![]() ,
,![]() 越大,说明两个分类变量有关系的可能性越大.
越大,说明两个分类变量有关系的可能性越大.
试题解析:(1)由题意可得列联表如下:
年龄层次 | 赞成“留欧” | 反对“留欧” | 合计 |
18岁~49岁 | 20 | 6 | 26 |
50岁及50岁以上 | 10 | 14 | 24 |
合计 | 30 | 20 | 50 |
(2)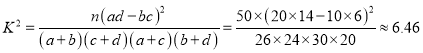 ,
,
∵![]() ,
,
∴有97.5%的把握认为赞成“留欧”与年龄层次有关
-
科目: 来源: 题型:
查看答案和解析>>【题目】心理学家发现,学生的接受能力依赖于老师引入概念和描述问题所用的时间,上课开始时,学生的兴趣激增,中间有一段不太长的时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散,并趋于稳定.分析结果和实验表明,设提出和讲述概念的时间为
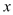 (单位:分),学生的接受能力为
(单位:分),学生的接受能力为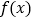 (
(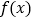 值越大,表示接受能力越强),
值越大,表示接受能力越强),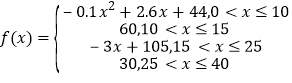
(1)开讲后多少分钟,学生的接受能力最强?能维持多少时间?
(2)试比较开讲后5分钟、20分钟、35分钟,学生的接受能力的大小;(3)若一个数学难题,需要56的接受能力以及12分钟时间,老师能否及时在学生一直达到所需接受能力的状态下讲述完这个难题?
-
科目: 来源: 题型:
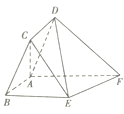
查看答案和解析>>【题目】如图,在平行四边形
 中,
中,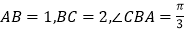 ,四边形
,四边形 为直角梯形,
为直角梯形,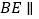 ∥
∥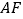 ,
,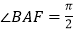 ,
,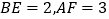 , 平面
, 平面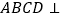 平面
平面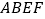 .
.
(1)求证:
 ;
;(2)求平面
 与平面
与平面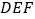 所成锐二面角的余弦值.
所成锐二面角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
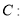
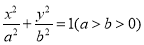 过点
过点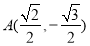 ,离心率为
,离心率为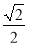 ,
,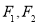 分别为左右焦点.
分别为左右焦点.(1)求椭圆
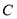 的标准方程;
的标准方程;(2)若
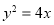 上存在两个点
上存在两个点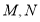 ,椭圆上有两个点
,椭圆上有两个点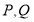 满足
满足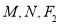 三点共线,
三点共线,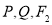 三点共线,且
三点共线,且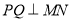 ,求四边形
,求四边形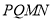 面积的取值范围.
面积的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
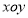 中,已知点
中,已知点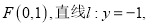
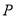 为平面上的动点,且过点
为平面上的动点,且过点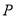 作
作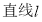 的垂线,垂足为
的垂线,垂足为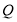 ,满足:
,满足: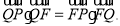
(Ⅰ)求动点
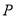 的轨迹
的轨迹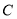 的方程;
的方程;(Ⅱ)在轨迹
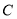 上求一点
上求一点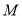 ,使得
,使得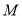 到直线
到直线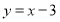 的距离最短,并求出最短距离.
的距离最短,并求出最短距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E为正方形ABCD边CD上异于点C,D的动点,将△ADE沿AE翻折成△SAE,使得平面SAE⊥平面ABCE,则下列三个说法中正确的个数是( )

①存在点E使得直线SA⊥平面SBC
②平面SBC内存在直线与SA平行
③平面ABCE内存在直线与平面SAE平行
A.0 B.1 C.2 D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 其中
其中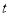 是实数.设
是实数.设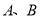 为该函数图像上的两点,横坐标分别为
为该函数图像上的两点,横坐标分别为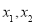 ,且
,且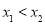 .
.(1求
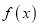 的单调区间和极值;
的单调区间和极值;(2)若
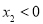 ,函数
,函数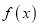 的图像在点
的图像在点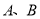 处的切线互相垂直,求
处的切线互相垂直,求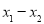 的最大值.
的最大值.
相关试题

