【题目】如图所示,在三棱锥A-BOC中,OA⊥底面BOC,∠OAB=∠OAC=30°,AB=AC=4,BC=![]() ,动点D在线段AB上.
,动点D在线段AB上.
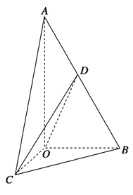
(1)求证:平面COD⊥平面AOB;
(2)当OD⊥AB时,求三棱锥C-OBD的体积.
参考答案:
【答案】(1)详见解析(2) ![]()
【解析】
试题分析:(1)欲证平面COD⊥平面AOB,根据面面垂直的判定定理可知在平面COD内一直线与平面AOB垂直,根据勾股定理可知OC⊥OB,根据线面垂直的判定定理可知OC⊥平面AOB,而OC平面COD,满足定理所需条件;(2)OD⊥AB,OD=![]() ,此时,BD=1.根据三棱锥的体积公式求出所求即可
,此时,BD=1.根据三棱锥的体积公式求出所求即可
试题解析:(1)∵AO⊥底面BOC,
∴AO⊥OC,
AO⊥OB.
∵∠OAB=∠OAC=30°,AB=AC=4,
∴OC=OB=2.
又BC=2![]() ,
,
∴OC⊥OB,
∴OC⊥平面AOB.
∵OC![]() 平面COD,
平面COD,
∴平面COD⊥平面AOB.
(2)∵OD⊥AB,∴BD=1,OD=![]() .
.
∴VC-OBD = ![]()
![]() ×
×![]() ×
×![]() ×1×2=
×1×2=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】若某产品的直径长与标准值的差的绝对值不超过1mm时,则视为合格品,否则视为不合格品.在近期一次产品抽样检查中,从某厂生产的此种产品中,随机抽取5000件进行检测,结果发现有50件不合格品.计算这50件不合格品的直径长与标准值的差(单位:mm),将所得数据分组,得到如下频率分布表:

(1)将上面表格中缺少的数据填在相应位置上;
(2)估计该厂生产的此种产品中,不合格品的直径长与标准值的差落在区间(1,3]内的概率;
(3)现对该厂这种产品的某个批次进行检查,结果发现有20件不合格品.据此估算这批产品中的合格品的件数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知过点
 的动直线
的动直线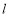 与圆
与圆 :
: 相交于
相交于 、
、 两点,
两点,  与直线
与直线 :
: 相交于
相交于 .
.
(1)当
 与
与 垂直时,求直线
垂直时,求直线 的方程,并判断圆心
的方程,并判断圆心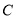 与直线
与直线 的位置关系;
的位置关系;(2)当
 时,求直线
时,求直线 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场有奖销售中,购满100元商品得1张奖券,多购多得,1000张奖券为一个开奖单位,设特等奖1个,一等奖10个,二等奖50个.设1张奖券中特等奖、一等奖、二等奖的事件分别为A、B、C,求:
(1)P(A),P(B),P(C);
(2)1张奖券的中奖概率;
(3)1张奖券不中特等奖且不中一等奖的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
 的底面
的底面 是矩形,平面
是矩形,平面 平面
平面 ,
,  是
是 的中点,且
的中点,且 ,
,  .
.
(I)求证:
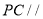 平面
平面 ;
;(II)求三棱锥
 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】投掷一个质地均匀的、每个面上标有一个数字的正方体玩具,它的六个面中,有两个面标的数字是0,两个面标的数字是2,两个面标的数字是4,将此玩具连续抛掷两次,以两次朝上一面的数字分别作为点P的横坐标和纵坐标.
(1)求点P落在区域C:x2+y2≤10内的概率;
(2)若以落在区域C上的所有点为顶点作面积最大的多边形区域M,在区域C上随机撒一粒豆子,求豆子落在区域M上的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 ,
, .
.(Ⅰ)当
 ,
, 时,设
时,设 ,求证:对任意的
,求证:对任意的 ,
, ;
;(Ⅱ)当
 时,若对任意
时,若对任意 ,不等式
,不等式 恒成立.求实数
恒成立.求实数 的取值范围.
的取值范围.
相关试题

