【题目】已知过点![]() 的动直线
的动直线![]() 与圆
与圆![]() :
:![]() 相交于
相交于![]() 、
、![]() 两点,
两点, ![]() 与直线
与直线![]() :
:![]() 相交于
相交于![]() .
.

(1)当![]() 与
与![]() 垂直时,求直线
垂直时,求直线![]() 的方程,并判断圆心
的方程,并判断圆心![]() 与直线
与直线![]() 的位置关系;
的位置关系;
(2)当![]() 时,求直线
时,求直线![]() 的方程.
的方程.
参考答案:
【答案】(1)直线l必过圆心C(2)![]() 或
或![]()
【解析】
试题分析:(1)根据直线m的一个法向量为(1,3),求得直线l的一个方向向量,由此求得l的点向式方程,可得直线l过圆心.(2)由|PQ|=![]() 得,圆心C到直线l的距离d=1,设直线l的方程为x-ny+1=0,求得n的值,可得直线l的方程.
得,圆心C到直线l的距离d=1,设直线l的方程为x-ny+1=0,求得n的值,可得直线l的方程.
试题解析:(1)∵![]() 与
与![]() 垂直,且
垂直,且![]() ,∴
,∴![]() ,
,
故直线![]() 方程为
方程为![]() ,即
,即![]() ………3分
………3分
圆心![]() 在
在![]() 上,理由是圆心坐标(0,3)满足直线
上,理由是圆心坐标(0,3)满足直线![]() 方程……………5分
方程……………5分
(2)①当直线![]() 与
与![]() 轴垂直时, 易知
轴垂直时, 易知![]() 符合题意………6分
符合题意………6分
②当直线![]() 与
与![]() 轴不垂直时, 设直线
轴不垂直时, 设直线![]() 的方程为
的方程为![]() ,即
,即![]() ,……7分
,……7分
∵![]() ,∴
,∴![]() ,……………8分
,……………8分
则由![]() ,得
,得![]() , ∴直线
, ∴直线![]() :
:![]() .………11分
.………11分
故直线![]() 的方程为
的方程为![]() 或
或![]() …………………12分
…………………12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校对任课教师的年龄状况和接受教育程度(学历)做调研,其部分结果(人数分布)如表:
学历
35岁以下
35~50岁
50岁以上
本科
80
30
20
研究生
x
20
y
(1)用分层抽样的方法在35~50岁年龄段的教师中抽取一个容量为5的样本,将该样本看成一个总体,从中任取2人,求至少有1人的学历为研究生的概率;
(2)若按年龄状况用分层抽样的方法抽取N个人,其中35岁以下48人,50岁以上10人,再从这N个人中随机抽取出1人,此人的年龄为50岁以上的概率为
 ,求x、y的值.
,求x、y的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知圆
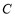 的极坐标方程为
的极坐标方程为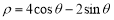 ,直线
,直线 的参数方程为
的参数方程为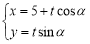 (
(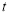 为参数).若直线
为参数).若直线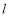 与圆
与圆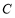 相交于不同的两点
相交于不同的两点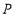 ,
,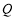 .
.(Ⅰ)写出圆
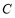 的直角坐标方程,并求圆心的坐标与半径;
的直角坐标方程,并求圆心的坐标与半径;(Ⅱ)若弦长
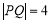 ,求直线
,求直线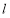 的斜率.
的斜率. -
科目: 来源: 题型:
查看答案和解析>>【题目】若某产品的直径长与标准值的差的绝对值不超过1mm时,则视为合格品,否则视为不合格品.在近期一次产品抽样检查中,从某厂生产的此种产品中,随机抽取5000件进行检测,结果发现有50件不合格品.计算这50件不合格品的直径长与标准值的差(单位:mm),将所得数据分组,得到如下频率分布表:

(1)将上面表格中缺少的数据填在相应位置上;
(2)估计该厂生产的此种产品中,不合格品的直径长与标准值的差落在区间(1,3]内的概率;
(3)现对该厂这种产品的某个批次进行检查,结果发现有20件不合格品.据此估算这批产品中的合格品的件数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场有奖销售中,购满100元商品得1张奖券,多购多得,1000张奖券为一个开奖单位,设特等奖1个,一等奖10个,二等奖50个.设1张奖券中特等奖、一等奖、二等奖的事件分别为A、B、C,求:
(1)P(A),P(B),P(C);
(2)1张奖券的中奖概率;
(3)1张奖券不中特等奖且不中一等奖的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在三棱锥A-BOC中,OA⊥底面BOC,∠OAB=∠OAC=30°,AB=AC=4,BC=
 ,动点D在线段AB上.
,动点D在线段AB上.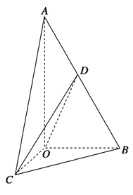
(1)求证:平面COD⊥平面AOB;
(2)当OD⊥AB时,求三棱锥C-OBD的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
 的底面
的底面 是矩形,平面
是矩形,平面 平面
平面 ,
,  是
是 的中点,且
的中点,且 ,
,  .
.
(I)求证:
 平面
平面 ;
;(II)求三棱锥
 的体积.
的体积.
相关试题

