【题目】投掷一个质地均匀的、每个面上标有一个数字的正方体玩具,它的六个面中,有两个面标的数字是0,两个面标的数字是2,两个面标的数字是4,将此玩具连续抛掷两次,以两次朝上一面的数字分别作为点P的横坐标和纵坐标.
(1)求点P落在区域C:x2+y2≤10内的概率;
(2)若以落在区域C上的所有点为顶点作面积最大的多边形区域M,在区域C上随机撒一粒豆子,求豆子落在区域M上的概率.
参考答案:
【答案】(1) ![]() (2)
(2) ![]()
【解析】
试题分析:(1)本小题是古典概型问题,欲求出点P落在区域C:x2+y2≤10内的概率,只须求出满足:x2+y2≤10上的点P的坐标有多少个,再将求得的值与整个点P的坐标个数求比值即得.(2)本小题是几何概型问题,欲求豆子落在区域M上的概率,只须求出满足:“豆子落在区域M上的概率”的区域的面积,再将求得的面积值与整个区域C的面积求比值即得
试题解析:(1)以0、2、4为横、纵坐标的点P有(0,0)、(0,2)、(0,4)、(2,0)、(2,2)、(2,4)、(4,0)、(4,2)、(4,4)共9个,而这些点中,落在区域C内的点有:(0,0)、(0,2)、(2,0)、(2,2)共4个,∴所求概率为P=![]() .
.
(2)∵区域M的面积为4,而区域C的面积为10π,
∴所求概率为P=![]() =
=![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场有奖销售中,购满100元商品得1张奖券,多购多得,1000张奖券为一个开奖单位,设特等奖1个,一等奖10个,二等奖50个.设1张奖券中特等奖、一等奖、二等奖的事件分别为A、B、C,求:
(1)P(A),P(B),P(C);
(2)1张奖券的中奖概率;
(3)1张奖券不中特等奖且不中一等奖的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在三棱锥A-BOC中,OA⊥底面BOC,∠OAB=∠OAC=30°,AB=AC=4,BC=
 ,动点D在线段AB上.
,动点D在线段AB上.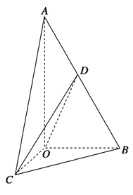
(1)求证:平面COD⊥平面AOB;
(2)当OD⊥AB时,求三棱锥C-OBD的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
 的底面
的底面 是矩形,平面
是矩形,平面 平面
平面 ,
,  是
是 的中点,且
的中点,且 ,
,  .
.
(I)求证:
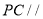 平面
平面 ;
;(II)求三棱锥
 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 ,
, .
.(Ⅰ)当
 ,
, 时,设
时,设 ,求证:对任意的
,求证:对任意的 ,
, ;
;(Ⅱ)当
 时,若对任意
时,若对任意 ,不等式
,不等式 恒成立.求实数
恒成立.求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的两个焦点与短轴的一个端点是等边三角形的三个顶点,且长轴长为4.
的两个焦点与短轴的一个端点是等边三角形的三个顶点,且长轴长为4.(1)求椭圆
 的方程;
的方程;(2)若
 是椭圆
是椭圆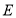 的左顶点,经过左焦点
的左顶点,经过左焦点 的直线
的直线 与椭圆
与椭圆 交于
交于 ,
, 两点,求
两点,求 与
与 的面积之差的绝对值的最大值.(
的面积之差的绝对值的最大值.( 为坐标原点)
为坐标原点) -
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某工厂开展群众体育活动的情况,拟采用分层抽样的方法从A,B,C三个区中抽取7个工厂进行调查,已知A,B,C区中分别有18,27,18个工厂
(Ⅰ)求从A,B,C区中分别抽取的工厂个数;
(Ⅱ)若从抽取的7个工厂中随机抽取2个进行调查结果的对比,求这2个工厂中至少有1个来自A区的概率。
相关试题

