【题目】证明与化简.
(1)求证:cotα=tanα+2cot2α;
(2)请利用(1)的结论证明:cotα=tanα+2tan2α+4cot4α;
(3)请你把(2)的结论推到更一般的情形,使之成为推广后的特例,并加以证明:
(4)化简:tan5°+2tan10°+4tan20°+8tan50°.
参考答案:
【答案】
(1)证明:tanα+2cot2α=tanα+ ![]()
=tanα+2× ![]()
=tanα+ ![]() ﹣tanα
﹣tanα
=cotα,
∴cotα=tanα+2cot2α.
(2)证明:∵cotα=tanα+2cot2α,
∴tanα+2tan2α+4cot4α
=cotα﹣2cot2α+2cos2α﹣4cot4α+4cot4α
=cotα,
∴cotα=tanα+2tan2α+4cot4α
(3)证明:一般地,cotα=tanα+2tan2α+22tan22α+…+2n﹣1tan2n﹣1α+2ncot2nα,n∈N*.
证明:∵cotα=tanα+2cot2α,∴cot2α=tan2α+2cot4α,
∴cotα=tanα+2tan2α+4cot4α=tanα+2tan2α+22cot22α,
以此类推得cotα=tanα+2tan2α+22tan22α+…+2n﹣1tan2n﹣1α+2ncot2nα,n∈N*
(4)解:tan5°+2tan10°+4tan20°+8tan50°
=tan5°+2tan10°+4tan20°+8cot40°
=cot5°.
【解析】(1)tanα+2cot2α=tanα+2× ![]() ,由此能证明cotα=tanα+2cot2α.(2)由cotα=tanα+2cot2α,得到tanα+2tan2α+4cot4α=cotα﹣2cot2α+2cos2α﹣4cot4α+4cot4α,由此能证明cotα=tanα+2tan2α+4cot4α.(3)一般地,cotα=tanα+2tan2α+22tan22α+…+2n﹣1tan2n﹣1α+2ncot2nα,n∈N* . 再由合情推量进行证明.(4)利用(3)的一般结论直接化简.
,由此能证明cotα=tanα+2cot2α.(2)由cotα=tanα+2cot2α,得到tanα+2tan2α+4cot4α=cotα﹣2cot2α+2cos2α﹣4cot4α+4cot4α,由此能证明cotα=tanα+2tan2α+4cot4α.(3)一般地,cotα=tanα+2tan2α+22tan22α+…+2n﹣1tan2n﹣1α+2ncot2nα,n∈N* . 再由合情推量进行证明.(4)利用(3)的一般结论直接化简.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在R上的函数f(x)=Asin(ωx+φ)(x>0,A>0)的图象如图所示.
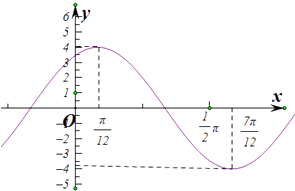
(1)求函数f(x)的解析式;
(2)写出函数f(x)的单调递增区间
(3)设不相等的实数,x1 , x2∈(0,π),且f(x1)=f(x2)=﹣2,求x1+x2的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】关于平面向量,有下列四个命题:
①若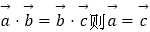 .
.
②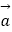 =(1,1),
=(1,1), 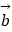 =(2,x),若
=(2,x),若 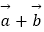 与
与 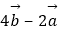 平行,则x=2.
平行,则x=2.
③非零向量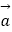 和
和 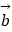 满足|
满足| 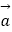 |=|
|=| 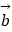 |=|
|=| 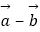 |,则
|,则 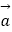 与
与 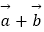 的夹角为60°.
的夹角为60°.
④点A(1,3),B(4,﹣1),与向量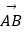 同方向的单位向量为(
同方向的单位向量为( 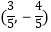 ).
).
其中真命题的序号为 . (写出所有真命题的序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=(x-3)ex+ax,aR
(1)当a=1时,求曲线f(x)在点(2,f(2))处的切线方程;
(2)当a[0,e)时,设函数f(x)在(1,+)上的最小值为g(a),求函数g(a)的值域.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将函数y=sinx的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象向左平移
 个单位,得到的图象对应的解析式是( )
个单位,得到的图象对应的解析式是( )
A.y=sin(2x+ )
)
B.y=sin( x+
x+  )
)
C.y=sin( x+
x+  )
)
D.y=sin(2x+ )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆F1:(x+1)2+y2=16,定点F2(1,0),A是圆F1上的一动点,线段F2A的垂直平分线交半径F1A于P点.
(1)求P点的轨迹C的方程;
(2)四边形EFGH的四个顶点都在曲线C上,且对角线EG,FH过原点O,
若kEGkFH=-
 ,求证:四边形EFGH的面积为定值,并求出此定值.
,求证:四边形EFGH的面积为定值,并求出此定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在三棱柱ABC-A1B1C1中,AA1B1B为正方形,BB1C1C为菱形,B1CAC1
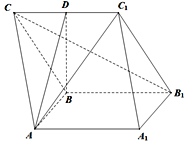
(Ⅰ)求证:平面AA1B1B面BB1C1C;
(Ⅱ)若D是CC1中点,ADB是二面角A-CC1-B的平面角,求直线AC1与平面ABC所成角的余弦值.
相关试题

