【题目】如图所示,在三棱柱ABC-A1B1C1中,AA1B1B为正方形,BB1C1C为菱形,B1CAC1
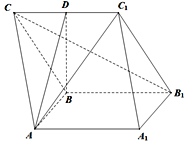
(Ⅰ)求证:平面AA1B1B面BB1C1C;
(Ⅱ)若D是CC1中点,ADB是二面角A-CC1-B的平面角,求直线AC1与平面ABC所成角的余弦值.
参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)先证明![]() , 从而
, 从而![]() ,结合
,结合![]() 可得
可得![]() ,进而可得结论;(2)分别以
,进而可得结论;(2)分别以![]() 为
为![]() 轴建立空间直角坐标系,分别求出平面
轴建立空间直角坐标系,分别求出平面![]() 的一个法向量及直线的AC1一个方向向量,根据空间向量夹角余弦公式,可得结果.
的一个法向量及直线的AC1一个方向向量,根据空间向量夹角余弦公式,可得结果.
试题解析:(1)连结![]() ,因为
,因为![]() 为菱形,所以
为菱形,所以![]() ,又
,又![]()
![]() ,
, ![]() ,所以
,所以![]() ,
,
故![]() 。
。
因为![]() ,且
,且![]() ,所以
,所以![]() ,
,
而![]() ,所以平面
,所以平面![]() 平面
平面![]() ;
;
(2)因为![]() 是二面角
是二面角![]() 的平面角,所以
的平面角,所以![]() ,又
,又![]() 是
是![]() 中点,所以
中点,所以![]() ,所以
,所以![]() 为等边三角形。
为等边三角形。
如图如示,分别以![]() 为
为![]() 轴建立空间直角坐标系。
轴建立空间直角坐标系。
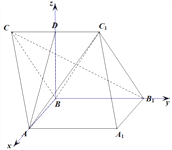
不妨设![]() ,则
,则![]() ,
,![]() 。
。
设![]() 是平面
是平面![]() 的一个法向量,则
的一个法向量,则
![]() ,即
,即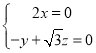 ,
,
取![]() 得
得![]()
所以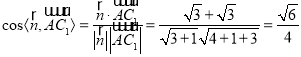 ,
,
所以直线![]() 与平面
与平面![]() 所成角的余弦值为
所成角的余弦值为![]() 。
。
-
科目: 来源: 题型:
查看答案和解析>>【题目】证明与化简.
(1)求证:cotα=tanα+2cot2α;
(2)请利用(1)的结论证明:cotα=tanα+2tan2α+4cot4α;
(3)请你把(2)的结论推到更一般的情形,使之成为推广后的特例,并加以证明:
(4)化简:tan5°+2tan10°+4tan20°+8tan50°. -
科目: 来源: 题型:
查看答案和解析>>【题目】将函数y=sinx的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象向左平移
 个单位,得到的图象对应的解析式是( )
个单位,得到的图象对应的解析式是( )
A.y=sin(2x+ )
)
B.y=sin( x+
x+  )
)
C.y=sin( x+
x+  )
)
D.y=sin(2x+ )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆F1:(x+1)2+y2=16,定点F2(1,0),A是圆F1上的一动点,线段F2A的垂直平分线交半径F1A于P点.
(1)求P点的轨迹C的方程;
(2)四边形EFGH的四个顶点都在曲线C上,且对角线EG,FH过原点O,
若kEGkFH=-
 ,求证:四边形EFGH的面积为定值,并求出此定值.
,求证:四边形EFGH的面积为定值,并求出此定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图所示的程序框图

(1)当输入的x为2,﹣1时,分别计算输出的y值,并写出输出值y关于输入值x的函数关系式;
(2)当输出的结果为4时,求输入的x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某小学对五年级的学生进行体质测试,已知五年一班共有学生30人,测试立定跳远的成绩用茎叶图表示如图(单位:cm): 男生成绩在175cm以上(包括175cm)定义为“合格”,成绩在175cm以下(不包括175cm)定义为“不合格”.
女生成绩在165cm以上(包括165cm)定义为“合格”,成绩在165cm以下(不包括165cm)定义为“不合格”.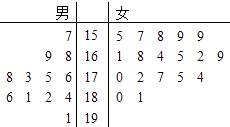
(1)求五年一班的女生立定跳远成绩的中位数;
(2)在五年一班的男生中任意选取3人,求至少有2人的成绩是合格的概率;
(3)若从五年一班成绩“合格”的学生中选取2人参加复试,用X表示其中男生的人数,写出X的分布列,并求X的数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=
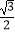 cos2x+sin2(x+
cos2x+sin2(x+  ). (Ⅰ)求f(x)的最小正周期和单调递增区间;
). (Ⅰ)求f(x)的最小正周期和单调递增区间;
(Ⅱ)当x∈[﹣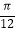 ,
, 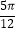 )时,求f(x)的取值范围.
)时,求f(x)的取值范围.
相关试题

