【题目】某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220.240),[240,260),[260,280),[280,300)分组的频率分布直方图如图. 
(1)求直方图中x的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为,[220,240),[240,260),[260,280),[280,300)的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在[220,240)的用户中应抽取多少户?
参考答案:
【答案】
(1)解:由直方图的性质可得(0.002+0.0095+0.011+0.0125+x+0.005+0.0025)×20=1,
解方程可得x=0.0075,∴直方图中x的值为0.0075
(2)解:月平均用电量的众数是 ![]() =230,
=230,
∵(0.002+0.0095+0.011)×20=0.45<0.5,
∴月平均用电量的中位数在[220,240)内,
设中位数为a,由(0.002+0.0095+0.011)×20+0.0125×(a﹣220)=0.5可得a=224,
∴月平均用电量的中位数为224
(3)解:月平均用电量为[220,240)的用户有0.0125×20×100=25,
月平均用电量为[240,260)的用户有0.0075×20×100=15,
月平均用电量为[260,280)的用户有0.005×20×100=10,
月平均用电量为[280,300)的用户有0.0025×20×100=5,
∴抽取比例为 ![]() =
= ![]() ,
,
∴月平均用电量在[220,240)的用户中应抽取25× ![]() =5户
=5户
【解析】(1)由直方图的性质可得(0.002+0.0095+0.011+0.0125+x+0.005+0.0025)×20=1,解方程可得;(2)由直方图中众数为最高矩形上端的中点可得,可得中位数在[220,240)内,设中位数为a,解方程(0.002+0.0095++0.011)×20+0.0125×(a﹣220)=0.5可得;(3)可得各段的用户分别为25,15,10,5,可得抽取比例,可得要抽取的户数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=120°,AC=3,△ABC的面积等于
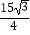 ,D为边长BC上一点.
,D为边长BC上一点. 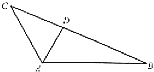
(1)求BC的长;
(2)当AD=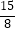 时,求cos∠CAD的值.
时,求cos∠CAD的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两艘轮船都要在某个泊位停靠6小时,假定它们在一昼夜的时间段中随机到达,则这两艘船中至少有一艘在停靠泊位时必须等待的概率是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分14分)如图,已知椭圆
 :
: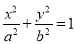 ,其左右焦点为
,其左右焦点为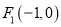 及
及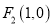 ,过点
,过点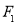 的直线交椭圆
的直线交椭圆 于
于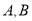 两点,线段
两点,线段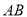 的中点为
的中点为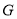 ,
,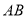 的中垂线与
的中垂线与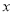 轴和
轴和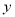 轴分别交于
轴分别交于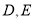 两点,且
两点,且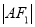 、
、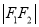 、
、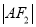 构成等差数列.
构成等差数列.
(1)求椭圆
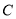 的方程;
的方程;(2)记△
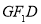 的面积为
的面积为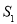 ,△
,△ (
(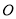 为原点)的面积为
为原点)的面积为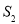 .试问:是否存在直线
.试问:是否存在直线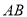 ,使得
,使得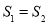 ?说明理由.
?说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分
 分)设数列
分)设数列 的前
的前 项和为
项和为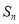 ,已知
,已知 ,
, ,
, .
.(1)求数列
 的通项公式;
的通项公式;(2)证明:对一切正整数
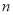 ,有
,有 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分12分)某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上
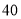 件产品作为样本称出它们的重量(单位:克),重量的分组区间为
件产品作为样本称出它们的重量(单位:克),重量的分组区间为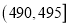 ,
,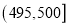 , ,
, ,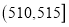 ,由此得到样本的频率分布直方图,如图所示.
,由此得到样本的频率分布直方图,如图所示.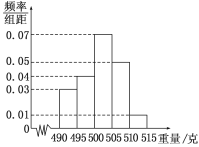
(1)根据频率分布直方图,求重量超过
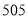 克的产品数量;
克的产品数量;(2)在上述抽取的
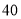 件产品中任取
件产品中任取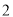 件,设
件,设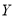 为重量超过
为重量超过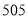 克的产品数量,求
克的产品数量,求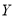 的分布列;
的分布列;(3)从该流水线上任取
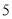 件产品,求恰有
件产品,求恰有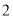 件产品的重量超过
件产品的重量超过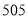 克的概率.
克的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】记等比数列{an}前n项和为Sn , 已知a1+a3=30,3S1 , 2S2 , S3成等差数列.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足b1=3,bn+1﹣3bn=3an , 求数列{bn}的前n项和Bn;
(3)删除数列{an}中的第3项,第6项,第9项,…,第3n项,余下的项按原来的顺序组成一个新数列,记为{cn},{cn}的前n项和为Tn , 若对任意n∈N* , 都有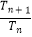 >a,试求实数a的最大值.
>a,试求实数a的最大值.
相关试题

