【题目】如图是某直三棱柱(侧棱与底面垂直的三棱柱)被削去上底后的直观图与三视图中的侧视图、俯视图,在直观图中, ![]() 是
是![]() 的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
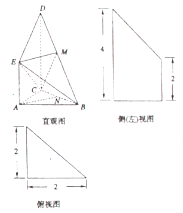
(1)求出该几何体的体积;
(2)若![]() 是
是![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() ;
;
参考答案:
【答案】(1) ![]() ;(2) 见解析.
;(2) 见解析.
【解析】试题分析:(1)先由面面垂直的性质定理证明![]() ,再由面面垂直的判定定理证明
,再由面面垂直的判定定理证明![]() 证明平面
证明平面![]() ,从而由棱锥的体积公式可得结果;(2)连接
,从而由棱锥的体积公式可得结果;(2)连接![]() ,由中位线定理得
,由中位线定理得![]() ,由平行四边形可得
,由平行四边形可得![]() ,进而可得结果.
,进而可得结果.
试题解析:(1)由题意可知:四棱锥![]() 中,
中,
平面![]() 平面
平面![]() ,
, ![]()
平面![]() 平面
平面![]()
所以, ![]() 平面
平面![]()
又![]() ,
, ![]() ,
,
则四棱锥![]() 的体积为:
的体积为: ![]()
(2)连接![]() ,则
,则![]() ,
, ![]()
又![]() ,所以四边形
,所以四边形![]() 为平心四边形,
为平心四边形, ![]()
![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以, ![]() 平面
平面![]()
【方法点晴】本题主要考查线面平行的判定定理、利用等积变换求三棱锥体积,属于难题.证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面. 本题(1)是就是利用方法①证明的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
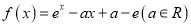 ,其中
,其中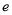 是自然对数的底数.
是自然对数的底数.(1)若
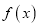 在
在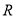 上为单调函数,求实数
上为单调函数,求实数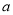 的取值范围;
的取值范围;(2)若
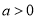 ,求证:
,求证: 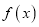 有唯一零点的充要条件是
有唯一零点的充要条件是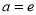 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,设P是圆
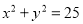 上的动点,点D是P在x轴上的投影,M为线段PD上一点,且
上的动点,点D是P在x轴上的投影,M为线段PD上一点,且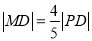 ,
,(1)当P在圆上运动时,求点M的轨迹C的方程;
(2)求过点(3,0)且斜率为
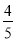 的直线被轨迹C所截线段的长度.
的直线被轨迹C所截线段的长度.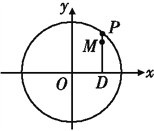
-
科目: 来源: 题型:
查看答案和解析>>【题目】在刚刚结束的五市联考中,某校对甲、乙两个文科班的数学成绩进行分析,规定:大于或等于120分为优秀,120分以下为非优秀,成绩统计后,得到如下的
 列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为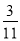 .
.班级
优秀
非优秀
合计
甲班
18
乙班
43
合计
110
(1)请完成上面的列联表;
(2)请问:是否有
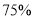 的把握认为“数学成绩与所在的班级有关系”?
的把握认为“数学成绩与所在的班级有关系”?(3)用分层抽样的方法从甲、乙两个文科班的数学成绩优秀的学生中抽取5名学生进行调研,然后再从这5名学生中随机抽取2名学生进行谈话,求抽到的2名学生中至少有1名乙班学生的概率.
参考公式:
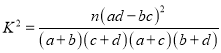 (其中
(其中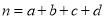 )
)参考数据:

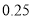

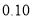
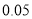
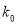

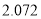
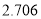
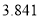
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,以坐标原点为极点,
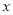 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线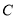 的极坐标方程为
的极坐标方程为 ,过点
,过点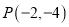 的直线
的直线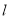 的参数方程为
的参数方程为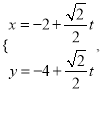 (
(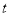 为参数),直线
为参数),直线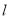 与曲线
与曲线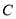 相交于
相交于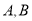 两点.
两点.(1)写出曲线
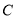 的直角坐标方程和直线
的直角坐标方程和直线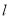 的普通方程;
的普通方程;(2)若
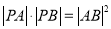 ,求
,求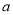 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
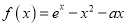 .
.(1)
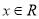 时,证明:
时,证明: 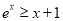 ;
;(2)当
 时,直线
时,直线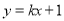 和曲线
和曲线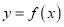 切于点
切于点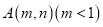 ,求实数
,求实数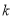 的值;
的值;(3)当
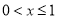 时,不等式
时,不等式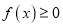 恒成立,求实数
恒成立,求实数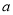 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】4月16日摩拜单车进驻大连市旅顺口区,绿色出行引领时尚,旅顺口区对市民进行“经常使用共享单车与年龄关系”的调查统计,若将单车用户按照年龄分为“年轻人”(20岁~39岁)和“非年轻人”(19岁及以下或者40岁及以上)两类,抽取一个容量为200的样本,将一周内使用的次数为6次或6次以上的称为“经常使用单车用户”。使用次数为5次或不足5次的称为“不常使用单车用户”,已知“经常使用单车用户”有120人,其中
 是“年轻人”,已知“不常使用单车用户”中有
是“年轻人”,已知“不常使用单车用户”中有 是“年轻人”.
是“年轻人”.(1)请你根据已知的数据,填写下列
 列联表:
列联表:年轻人
非年轻人
合计
经常使用单车用户
不常使用单车用户
合计
(2)请根据(1)中的列联表,计算
 值并判断能否有
值并判断能否有 的把握认为经常使用共享单车与年龄有关?
的把握认为经常使用共享单车与年龄有关?(附:

当
 时,有
时,有 的把握说事件
的把握说事件 与
与 有关;当
有关;当 时,有
时,有 的把握说事件
的把握说事件 与
与 有关;当
有关;当 时,认为事件
时,认为事件 与
与 是无关的)
是无关的)
相关试题

