【题目】已知椭圆![]() 与双曲线
与双曲线![]() 有共同焦点,且离心率为
有共同焦点,且离心率为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)设![]() 为椭圆
为椭圆![]() 的下顶点,
的下顶点, ![]() 为椭圆上异于
为椭圆上异于![]() 的不同两点,且直线
的不同两点,且直线![]() 与
与![]() 的斜率之积为
的斜率之积为![]() .
.
(ⅰ)试问![]() 所在直线是否过定点?若是,求出该定点;若不是,请说明理由;
所在直线是否过定点?若是,求出该定点;若不是,请说明理由;
(ⅱ)若![]() 为椭圆
为椭圆![]() 上异于
上异于![]() 的一点,且
的一点,且![]() ,求
,求![]() 的面积的最小值.
的面积的最小值.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)(ⅰ)(0,0);(ⅱ)
;(Ⅱ)(ⅰ)(0,0);(ⅱ)![]() .
.
【解析】试题分析:(Ⅰ)由题意设椭圆![]() 的方程为
的方程为![]() ,则
,则![]() ,
,
又![]() ,∴
,∴![]() ,∴
,∴![]() ,则椭圆
,则椭圆![]() 的方程可求:
的方程可求:
(Ⅱ)(ⅰ)讨论可知,直线![]() 的斜率存在,设
的斜率存在,设![]() 所在直线方程为
所在直线方程为![]() ,
,
联立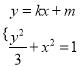 ,消去
,消去![]() 得:
得: ![]() ,①
,①
设![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,将上述结论代入可得
,将上述结论代入可得
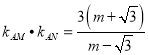 .又由题意
.又由题意![]()
解得: ![]() .即直线
.即直线![]() 恒过点(0,0).
恒过点(0,0).
(ⅱ)由(ⅰ)知![]() ,
, ![]() ,
,
而![]() ,∴
,∴![]() .
.
当![]() 时,设
时,设![]() 所在直线方程为
所在直线方程为![]() ,
,
则![]() ,
, ![]() ,
,
当![]() 时,亦符合上式,
时,亦符合上式,
∴![]()
![]()
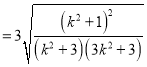 .
.
令![]() ,
, ![]() ,
,
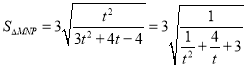 ,
,
∵![]() ,∴
,∴![]() ,
,
当![]() ,即
,即![]() 时,
时, ![]() 取最大值4,
取最大值4,
所以当![]() ,即
,即![]() 时,
时, ![]() 面积最小,最小值为
面积最小,最小值为![]() .
.
试题解析:(Ⅰ)由题意知:双曲线![]() 的焦点为
的焦点为![]() ,
, ![]() ,
,
设椭圆![]() 的方程为
的方程为![]() ,半焦距为
,半焦距为![]() ,则
,则![]() ,
,
又![]() ,∴
,∴![]() ,
,
∴![]()
∴椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)(ⅰ)若直线![]() 斜率不存在,设
斜率不存在,设![]() ,
, ![]() ,
,
则![]() ,
,
而![]() ,故不成立.
,故不成立.
所以直线![]() 的斜率存在,
的斜率存在,
设![]() 所在直线方程为
所在直线方程为![]() ,
,
联立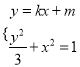 ,消去
,消去![]() 得:
得: ![]() ,①
,①
设![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
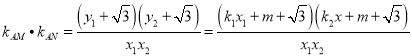
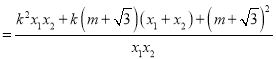
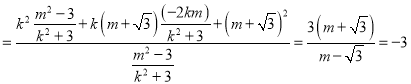 .
.
整理得: ![]() .
.
∴直线![]() 恒过点(0,0).
恒过点(0,0).
(ⅱ)由(ⅰ)知![]() ,
, ![]() ,
,
面![]() ,∴
,∴![]() .
.
当![]() 时,设
时,设![]() 所在直线方程为
所在直线方程为![]() ,
,
则![]() ,
, ![]() ,
,
当![]() 时,亦符合上式,
时,亦符合上式,
∴![]()
![]()
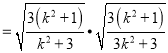
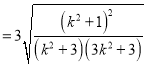 .
.
令![]() ,
, ![]() ,
,
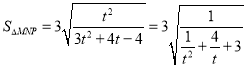 ,
,
∵![]() ,∴
,∴![]() ,
,
当![]() ,即
,即![]() 时,
时, ![]() 取最大值4,
取最大值4,
所以当![]() ,即
,即![]() 时,
时, ![]() 面积最小,最小值为
面积最小,最小值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
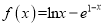 ,
,  .
.(Ⅰ)判断函数
 零点的个数,并说明理由;
零点的个数,并说明理由;(Ⅱ)记
 ,讨论
,讨论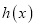 的单调性;
的单调性;(Ⅲ)若
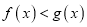 在
在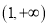 恒成立,求实数
恒成立,求实数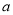 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,
,  .
.(1)求函数
 的极值;
的极值;(2)若函数
 在区间
在区间 内有两个零点,求
内有两个零点,求 的取值范围;
的取值范围;(3)求证:当
 时,
时,  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥
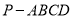 中,
中, 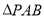 为正三角形,四边形
为正三角形,四边形 为矩形,平面
为矩形,平面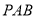
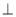 平面
平面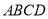 ,
, 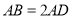 ,
, 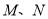 分别为
分别为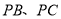 的中点。
的中点。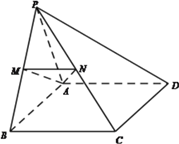
(Ⅰ)求证:
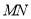 //平面
//平面 ;
;(Ⅱ)求二面角
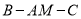 的大小。
的大小。 -
科目: 来源: 题型:
查看答案和解析>>【题目】某校举行汉字听写比赛,为了了解本次比赛成绩情况,从得分不低于50分的试卷中随机抽取100名学生的成绩(得分均为整数,满分100分)进行统计,请根据频率分布表中所提供的数据,解答下列问题:
组号
分组
频数
频率
第1组
[50,60)
5
0.05
第2组
[60,70)
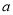
0.35
第3组
[70,80)
30
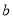
第4组
[80,90)
20
0.20
第5组
[90,100]
10
0.10
合计
100
1.00
(Ⅰ)求
 的值;
的值;(Ⅱ)若从成绩较好的第3、4、5组中按分层抽样的方法抽取6人参加市汉字听写比赛,并从中选出2人做种子选手,求2人中至少有1人是第4组的概率。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在投掷骰子试验中,根据向上的点数可以定义许多事件,如:A={出现1点},B={出现3点或4点},C={出现的点数是奇数},D={出现的点数是偶数}.
(1)说明以上4个事件的关系.
(2)求两两运算的结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场有奖销售中,购满100元商品得1张奖券,多购多得.1 000张奖券为一个开奖单位,设特等奖1个,一等奖10个,二等奖50个.设1张奖券中特等奖、一等奖、二等奖的事件分别为A,B,C,求:
(1)P(A),P(B),P(C).
(2)1张奖券的中奖概率.
(3)1张奖券不中特等奖,且不中一等奖的概率.
相关试题

