【题目】已知椭圆的中心是坐标原点![]() ,焦点在
,焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,又椭圆上任一点到两焦点的距离和为
,又椭圆上任一点到两焦点的距离和为![]() .过右焦点
.过右焦点![]() 与
与![]() 轴不垂直的直线
轴不垂直的直线![]() 交椭圆于
交椭圆于![]() ,
,![]() 两点.
两点.
(1)求椭圆的方程;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的取值范围;若不存在,请
的取值范围;若不存在,请
说明理由.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)根据椭圆的离心率,以及椭圆上任意一点到两焦点的距离和为![]() ,求出
,求出![]() 即可求出椭圆方程.(2)设出直线方程,联立直线方程和椭圆方程,转化为一元二次方程,利用根与系数的关系进行求解.
即可求出椭圆方程.(2)设出直线方程,联立直线方程和椭圆方程,转化为一元二次方程,利用根与系数的关系进行求解.
试题解析:(1)因为离心率为![]()
![]() ,
,
![]() 故椭圆的方程为:
故椭圆的方程为:![]()
(2)![]() 若
若![]() 与
与![]() 轴重合时,显然
轴重合时,显然![]() 与原点重合,
与原点重合,![]() 合条件
合条件
![]() 若直线
若直线![]() 的斜率
的斜率![]() ,则可设
,则可设![]() ,设
,设![]() 则:
则:
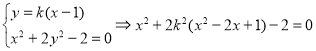
所以化简得:![]() ;
;
![]()
![]() 的中点横坐标为:
的中点横坐标为:![]() ,代入
,代入![]() 可得:
可得:
![]() 的中点为
的中点为![]()
![]() ,
,
由于![]() 得到
得到![]()
所以: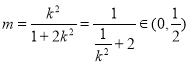 综合(1)(2)得到:
综合(1)(2)得到:![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】3名志愿者在10月1号至10月5号期间参加社区服务工作.
(1)若每名志愿者在这5天中任选一天参加社区服务工作,且各志愿者的选择互不影响,求3名志愿者恰好连续3天参加社区服务工作的概率;
(2)若每名志愿者在这5天中任选两天参加社区服务工作,且各志愿者的选择互不影响,记
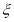 表示这3名志愿者在10月1号参加社区服务工作的人数,求随机变量
表示这3名志愿者在10月1号参加社区服务工作的人数,求随机变量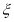 的分布列.
的分布列. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
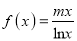 ,曲线
,曲线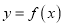 在点
在点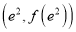 处的切线与直线
处的切线与直线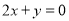 垂直(其中
垂直(其中 为自然对数的底数).
为自然对数的底数).(1)求
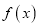 的解析式及单调递减区间;
的解析式及单调递减区间;(2)是否存在常数
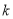 ,使得对于定义域内的任意
,使得对于定义域内的任意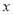 ,
, 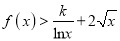 恒成立,若存在,求出
恒成立,若存在,求出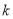 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的左、右焦点分别为
的左、右焦点分别为 ,短轴两个端点为
,短轴两个端点为 ,且四边形
,且四边形 是边长为2的正方形.
是边长为2的正方形.(1)求椭圆的方程;
(2)若
 分别是椭圆长轴的左、右端点,动点
分别是椭圆长轴的左、右端点,动点 满足
满足 ,连结
,连结 ,交椭圆于点
,交椭圆于点 ,证明:
,证明: 为定值;
为定值;(3)在(2)的条件下,试问
 轴上是否存在异于点
轴上是否存在异于点 的定点
的定点 ,使得以
,使得以 为直径的圆恒过直线
为直径的圆恒过直线 的交点,若存在,求出点
的交点,若存在,求出点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
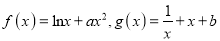 ,且直线
,且直线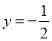 是函数
是函数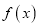 的一条切线.
的一条切线.(1)求
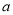 的值;
的值;(2)对任意的
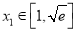 ,都存在
,都存在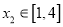 ,使得
,使得 ,求
,求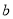 的取值范围;
的取值范围;(3)已知方程
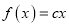 有两个根
有两个根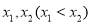 ,若
,若 ,求证:
,求证: 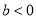 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某投资公司拟投资开发某项新产品,市场评估能获得10~1 000万元的投资收益.现公司准备制定一个对科研课题组的奖励方案:奖金y(单位:万元)随投资收益x(单位:万元)的增加而增加,且奖金不低于1万元,同时不超过投资收益的20%.
(1) 设奖励方案的函数模型为f(x),试用数学语言表述公司对奖励方案的函数模型f(x)的基本要求;
(2) 公司能不能用函数f(x)=
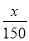 +2作为预设的奖励方案的模型函数?
+2作为预设的奖励方案的模型函数? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a=(1,2),b=(-2,n),a与b的夹角是45°.
(1) 求b;
(2) 若c与b同向,且a与c-a垂直,求向量c的坐标.
相关试题

