【题目】以下四个命题中:
①某地市高三理科学生有15000名,在一次调研测试中,数学成绩 ![]() 服从正态分布
服从正态分布 ![]() ,已知
,已知 ![]() ,若按成绩分层抽样的方式抽取100份试卷进行分析,则应从120分以上(包括120分)的试卷中抽取
,若按成绩分层抽样的方式抽取100份试卷进行分析,则应从120分以上(包括120分)的试卷中抽取 ![]() 份;
份;
②已知命题 ![]() ,则
,则 ![]() :
: ![]() ;
;
③在 ![]() 上随机取一个数
上随机取一个数 ![]() ,能使函数
,能使函数 ![]() 在
在 ![]() 上有零点的概率为
上有零点的概率为 ![]() ;
;
④设 ![]() ,则“
,则“ ![]() ”是“
”是“ ![]() ”的充要条件.
”的充要条件.
其中真命题的序号为.
参考答案:
【答案】②③
【解析】①∵ ![]()
∴应从120分以上(包括120分)的试卷中抽取100×0.1=10(份),故①为假命题;
②由全称命题的否定是特称命题知, ![]() 为
为 ![]() ,故②为真命题;
,故②为真命题;
③若 ![]() 有零点,则
有零点,则 ![]() ,解得m≥2或m≤-2,由几何概率计算公式可得在
,解得m≥2或m≤-2,由几何概率计算公式可得在 ![]() 上随机去一个数m,能使函数
上随机去一个数m,能使函数 ![]() 在R上有零点的概率为
在R上有零点的概率为 ![]() ,故③为真命题;
,故③为真命题;
④ ![]() ,所以“
,所以“ ![]() ”是“
”是“ ![]() >1”的充分不必要条件,故④为假命题.
>1”的充分不必要条件,故④为假命题.
故填②③.
【考点精析】利用函数的零点与方程根的关系对题目进行判断即可得到答案,需要熟知二次函数的零点:(1)△>0,方程 有两不等实根,二次函数的图象与 轴有两个交点,二次函数有两个零点;(2)△=0,方程 有两相等实根(二重根),二次函数的图象与 轴有一个交点,二次函数有一个二重零点或二阶零点;(3)△<0,方程 无实根,二次函数的图象与 轴无交点,二次函数无零点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,把函数
,把函数  的图象向右平移
的图象向右平移  个单位,得到函数
个单位,得到函数  的图象,若
的图象,若  是
是  在
在  内的两根,则
内的两根,则  的值为( )
的值为( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设顶点在原点,焦点在
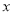 轴上的拋物线过点
轴上的拋物线过点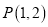 ,过
,过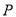 作抛物线的动弦
作抛物线的动弦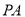 ,
, 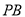 ,并设它们的斜率分别为
,并设它们的斜率分别为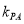 ,
, 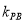 .
.(Ⅰ)求拋物线的方程;
(Ⅱ)若
 ,求证:直线
,求证:直线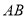 的斜率为定值,并求出其值;
的斜率为定值,并求出其值;(III)若
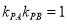 ,求证:直线
,求证:直线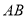 恒过定点,并求出其坐标.
恒过定点,并求出其坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
(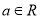 )在其定义域内有两个不同的极值点.
)在其定义域内有两个不同的极值点.(Ⅰ)求实数
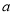 的取值范围;
的取值范围; (Ⅱ)记两个极值点分别为
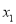 ,
, 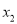 (
( ),求证:
),求证:  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】若关于
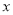 的不等式
的不等式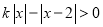 恰好有4个整数解,则实数
恰好有4个整数解,则实数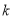 的取值范围是( )
的取值范围是( )A.
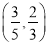 B.
B. 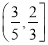 C.
C. 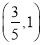 D.
D. 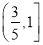
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列
 中,公差
中,公差  ,
,  ,且
,且  成等比数列.
成等比数列.
(1)求数列 的通项公式;
的通项公式;
(2)若 为数列
为数列  的前
的前  项和,且存在
项和,且存在  ,使得
,使得 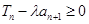 成立,求实数
成立,求实数  的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
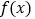 图象如图,
图象如图,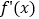 是
是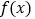 的导函数,则下列数值排序正确的是( )
的导函数,则下列数值排序正确的是( )
A.
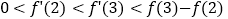
B.

C.
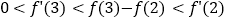
D.

【答案】C
【解析】结合函数的图像可知过点
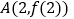 的切线的倾斜角最大,过点
的切线的倾斜角最大,过点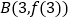 的切线的倾斜角最小,又因为点
的切线的倾斜角最小,又因为点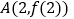 的切线的斜率
的切线的斜率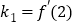 ,点
,点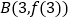 的切线斜率
的切线斜率 ,直线
,直线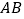 的斜率
的斜率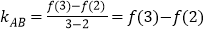 ,故
,故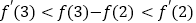 ,应选答案C。
,应选答案C。点睛:本题旨在考查导数的几何意义与函数的单调性等基础知识的综合运用。求解时充分借助题设中所提供的函数图形的直观,数形结合进行解答。先将经过两切点
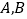 的直线绕点
的直线绕点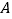 逆时针旋转到与函数的图像相切,再将经过两切点的直线绕点
逆时针旋转到与函数的图像相切,再将经过两切点的直线绕点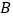 顺时针旋转到与函数的图像相切,这个过程很容易发现
顺时针旋转到与函数的图像相切,这个过程很容易发现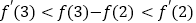 ,从而将问题化为直观图形的问题来求解。
,从而将问题化为直观图形的问题来求解。【题型】单选题
【结束】
9【题目】已知
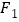 、
、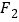 为双曲线
为双曲线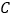 :
: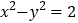 的左、右焦点,点
的左、右焦点,点 在
在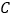 上,
上,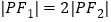 ,则
,则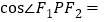 ( )
( )A.
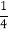 B.
B.  C.
C. 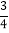 D.
D. 
相关试题

