【题目】选修4—5:不等式选讲
已知函数![]()
(1)当![]() 时,求不等式
时,求不等式![]() 的解集;
的解集;
(2)若![]() |的解集包含
|的解集包含![]() ,求
,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)当a=-3时, 根据分段函数的特点,即可求出f(x)3的解集;(2)f(x)|x-4||x-4|-|x-2||x+a|.当x[1,2]时,|x-4|-|x-2||x+a|-2-ax2-a,可求出满足条件的a的取值范围.
根据分段函数的特点,即可求出f(x)3的解集;(2)f(x)|x-4||x-4|-|x-2||x+a|.当x[1,2]时,|x-4|-|x-2||x+a|-2-ax2-a,可求出满足条件的a的取值范围.
试题解析:(1)当a=-3时,
当x2时,由f(x)3得-2x+53,解得:x1
当2<x<3时,f(x)3无解;
当x3时,由f(x)3得2x-53,解得x4;
所以f(x)3的解集为{x|x1}∪{x|x4} 5分
(2)f(x)|x-4||x-4|-|x-2||x+a|.
当x[1,2]时,|x-4|-|x-2||x+a|(4-x)-(2-x)|x+a| -2-ax2-a
由条件得:-2-a1且2-a2,即-3a0
故满足条件的a的取值范围为[-3,0] 10分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xOy中,圆C的参数方程
 (φ为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(φ为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.(Ⅰ)求圆C的极坐标方程;
(Ⅱ)直线l的极坐标方程是ρ(sinθ+
 )=3
)=3 ,射线OM:θ=
,射线OM:θ= 与圆C的交点为O,P,与直线l的交点为Q,求线段PQ的长.
与圆C的交点为O,P,与直线l的交点为Q,求线段PQ的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,已知cosC+(cosA﹣
 sinA)cosB=0.
sinA)cosB=0.
(1)求角B的大小;
(2)若a+c=1,求b的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】正项数列{an}的前n项和Sn满足:Sn2

(1)求数列{an}的通项公式an;
(2)令b ,数列{bn}的前n项和为Tn . 证明:对于任意n∈N* , 都有
,数列{bn}的前n项和为Tn . 证明:对于任意n∈N* , 都有  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】2017年5月14日.第一届“一带一路国际高峰论坛在北京举行,为了解不同年龄的人对“一带一路”关注程度,某机构随机抽取了年龄在15-75岁之间的100人进行调查,经统计“青少年”与“中老年” 的人数之比为9:11

(1)根据已知条件完成上面的列联表,并判断能否有99%的把握认为关注“一带一路”是和年龄段有关?
(2)现从抽取的青少年中采用分层抽样的办法选取9人进行问卷调查,在这9人中再取3人进打面对面询问,记选取的3人中“一带一路”的人数为X,求x的分布列及数学期望.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,若
中,若 ,
, ,
, 成等差数列,且三个内角
成等差数列,且三个内角 ,
, ,
, 也成等差数列,则
也成等差数列,则 的形状为__________.
的形状为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( ,
,  为自然对数的底数).
为自然对数的底数).(Ⅰ)求函数
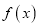 的极值;
的极值;(Ⅱ)当
 时,若直线
时,若直线 与曲线
与曲线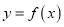 没有公共点,求
没有公共点,求 的最大值.
的最大值.
相关试题

