【题目】已知经过![]() 两点的圆
两点的圆![]() 半径小于5,且在
半径小于5,且在![]() 轴上截得的线段长为
轴上截得的线段长为![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)已知直线![]() ,若
,若![]() 与圆
与圆![]() 交于
交于![]() 两点,且以线段
两点,且以线段![]() 为直径的圆经过坐标原点,求直线
为直径的圆经过坐标原点,求直线![]() 的方程.
的方程.
参考答案:
【答案】(1) ![]() ;(2)
;(2) ![]() 或
或![]() .
.
【解析】试题分析:(1)设圆的一般方程为![]() ,因为直线过点
,因为直线过点![]() ,故
,故![]() ,又它截
,又它截![]() 轴所得的弦长为
轴所得的弦长为![]() ,故可得
,故可得![]() ,解方程组就可以得到
,解方程组就可以得到 ,从而圆的方程为
,从而圆的方程为![]() .(2)因为
.(2)因为![]() ,故设
,故设![]() ,再设
,再设![]() ,则以
,则以![]() 为直径的圆过原点可以转化为
为直径的圆过原点可以转化为![]() ,联立方程组消元后利用韦达定理把该关系式转化为关于
,联立方程组消元后利用韦达定理把该关系式转化为关于![]() 的方程即可解出
的方程即可解出![]() ,也就得到直线
,也就得到直线![]() 的方程.
的方程.
解析:(1)设圆的方程为![]() ,令
,令![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ① .又圆过
① .又圆过![]() 两点,故
两点,故![]() ,整理/span>
,整理/span>![]() ,消去
,消去![]() 得
得![]() ②,由①②得:
②,由①②得:  或
或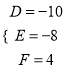 ,而圆的半径小于5,故
,而圆的半径小于5,故![]() ,故舍去
,故舍去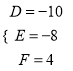 ,所以圆的方程为
,所以圆的方程为![]() .
.
(2)![]() ,设
,设![]() 的方程为:
的方程为: ![]() ,由
,由![]() ,消去
,消去![]() 得
得![]() .
.
设,则![]() .因为以
.因为以![]() 为直径的圆过原点,所以
为直径的圆过原点,所以![]() ,即
,即![]() ,故
,故![]() ,整理得:
,整理得: ![]() 或
或![]() ,当
,当![]() 或
或![]() 均满足
均满足![]() ,故
,故![]() 的方程为
的方程为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
,  .
.(1)当
 时,求函数
时,求函数 的图象在
的图象在 处的切线方程;
处的切线方程;(2)若函数
 在定义域上为单调增函数.
在定义域上为单调增函数.①求
 最大整数值;
最大整数值;②证明:
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列
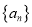 满足
满足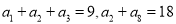 ,数列
,数列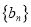 的前
的前 项和为
项和为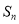 ,且满足
,且满足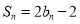 .
.(1)求数列
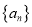 和
和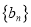 的通项公式;
的通项公式;(2)数列
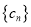 满足
满足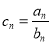 ,求数列
,求数列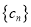 的前
的前 项和
项和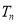 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)求函数
 的单调区间;
的单调区间;(2)若
 恒成立,试确定实数
恒成立,试确定实数 的取值范围;
的取值范围;(3)证明
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
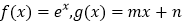 .
.(1)设
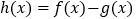 .
.①若函数
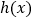 在
在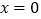 处的切线过点
处的切线过点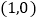 ,求
,求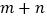 的值;
的值;②当
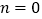 时,若函数
时,若函数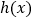 在
在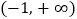 上没有零点,求
上没有零点,求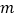 的取值范围.
的取值范围.(2)设函数
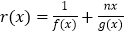 ,且
,且 ,求证: 当
,求证: 当 时,
时,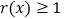 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校初三年级有
 名学生,随机抽查了
名学生,随机抽查了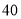 名学生,测试
名学生,测试 分钟仰卧起坐的成绩(次数),将数据整理后绘制成如图所示的频率分布直方图.用样本估计总体,下列结论正确的是( )
分钟仰卧起坐的成绩(次数),将数据整理后绘制成如图所示的频率分布直方图.用样本估计总体,下列结论正确的是( )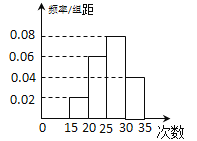
A. 该校初三年级学生
 分钟仰卧起坐的次数的中位数为
分钟仰卧起坐的次数的中位数为 次
次B. 该校初三年级学生
 分钟仰卧起坐的次数的众数为
分钟仰卧起坐的次数的众数为 次
次C. 该校初三年级学生
 分钟仰卧起坐的次数超过
分钟仰卧起坐的次数超过 次的人数约有
次的人数约有 人
人D. 该校初三年级学生
 分钟仰卧起坐的次数少于
分钟仰卧起坐的次数少于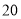 次的人数约为
次的人数约为 人.
人. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学调查了某班全部
 名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
(1)能否由
 的把握认为参加书法社团和参加演讲社团有关?
的把握认为参加书法社团和参加演讲社团有关?(附:

当
 时,有
时,有 的把握说事件
的把握说事件 与
与 有关;当
有关;当 ,认为事件
,认为事件 与
与 是无关的)
是无关的)(2)已知既参加书法社团又参加演讲社团的
 名同学中,有
名同学中,有 名男同学
名男同学 ,
,  ,
,  ,
,  ,
,  ,
,  名女同学
名女同学 ,
,  ,
,  .现从这
.现从这 名男同学和
名男同学和 名女同学中各随机选
名女同学中各随机选 人,求
人,求 被选中且
被选中且 未被选中的概率.
未被选中的概率.
相关试题

