【题目】已知函数![]() .
.
(1)设![]() .
.
①若函数![]() 在
在![]() 处的切线过点
处的切线过点![]() ,求
,求![]() 的值;
的值;
②当![]() 时,若函数
时,若函数![]() 在
在![]() 上没有零点,求
上没有零点,求![]() 的取值范围.
的取值范围.
(2)设函数![]() ,且
,且![]() ,求证: 当
,求证: 当![]() 时,
时,![]() .
.
参考答案:
【答案】(1)①![]() ;②
;②![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:(1)①由题意![]()
![]() 切线斜率
切线斜率![]() ,又
,又![]()
![]() 切线方程
切线方程![]()
![]()
![]() ;②当
;②当![]()
![]()
![]() ,因为
,因为![]() .
.
然后利用分类讨论思想对![]() 和
和![]() 分情况讨论的:
分情况讨论的:![]() ;(2)由题意得
;(2)由题意得![]() ,从而原命题等价于
,从而原命题等价于![]() 设
设![]()
![]()
![]() ,然后利用导数工具证明
,然后利用导数工具证明![]() .
.
试题解析:
(1)①由题意,得![]() ,所以函数
,所以函数![]() 在
在![]() 处的切线斜率
处的切线斜率![]() ,又
,又![]() ,所以函数
,所以函数![]() 在
在![]() 处的切线方程
处的切线方程![]() ,将点
,将点![]() 代入,得
代入,得![]() .
.
②当![]() ,可得
,可得![]() ,因为
,因为![]() .
.
当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上单调递增,而
上单调递增,而![]() ,所以只需
,所以只需![]() ,解得
,解得![]() ,从而
,从而![]() 当
当![]() 时,由
时,由![]() ,解得
,解得
![]() ,当
,当![]() 时,
时,![]() 单调递减; 当
单调递减; 当![]() 时,
时,![]() 单调递增, 所以函数
单调递增, 所以函数![]() 在
在![]() 上有最小值为
上有最小值为![]() ,令
,令![]() ,解得
,解得![]() .综上所述,
.综上所述,![]() .
.
(2)由题意, ,而
,而![]() ,等价于
,等价于
![]() ,则
,则![]() ,且
,且![]() ,
,
令![]() ,则
,则![]() ,因为
,因为![]() ,所以导数
,所以导数![]() 在
在![]() 上单调递增,于是
上单调递增,于是![]() ,从而函数
,从而函数![]() 在
在![]() 上单调递增,即
上单调递增,即![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某海域有
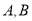 两个岛屿,
两个岛屿,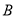 岛在
岛在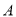 岛正东4海里处,经多年观察研究发现,某种鱼群洄游的路线是曲线
岛正东4海里处,经多年观察研究发现,某种鱼群洄游的路线是曲线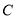 ,曾有渔船在距
,曾有渔船在距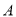 岛、
岛、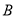 岛距离和为8海里处发出过鱼群。以
岛距离和为8海里处发出过鱼群。以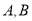 所在直线为
所在直线为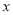 轴,
轴,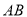 的垂直平分线为
的垂直平分线为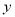 轴建立平面直角坐标系.
轴建立平面直角坐标系.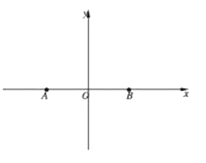
(1)求曲线
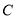 的标准方程;
的标准方程;(2)某日,研究人员在
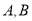 两岛同时用声纳探测仪发出不同频率的探测信号(传播速度相同),
两岛同时用声纳探测仪发出不同频率的探测信号(传播速度相同),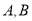 两岛收到鱼群在
两岛收到鱼群在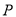 处反射信号的时间比为
处反射信号的时间比为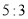 ,问你能否确定
,问你能否确定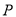 处的位置(即点
处的位置(即点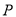 的坐标)?
的坐标)? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知三棱锥P-ABC中,∠ACB=90°,CB=4,AB=20,D为AB中点,M为PB中点,且△PDB是正三角形,PA⊥PC。
 .
.(1)求证:DM∥平面PAC;
(2)求证:平面PAC⊥平面ABC;
(3)求三棱锥M-BCD的体积
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某生态园将一三角形地块
 的一角
的一角 开辟为水果园种植桃树,已知角
开辟为水果园种植桃树,已知角 为
为 ,
,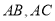 的长度均大于
的长度均大于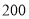 米,现在边界
米,现在边界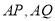 处建围墙,在
处建围墙,在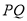 处围竹篱笆.
处围竹篱笆.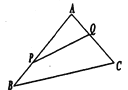
(1)若围墙
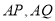 总 长度为
总 长度为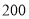 米,如何围可使得三角形地块
米,如何围可使得三角形地块 的面积最大?
的面积最大?(2)已知
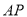 段围墙高
段围墙高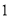 米,
米,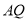 段围墙高
段围墙高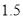 米,造价均为每平方米
米,造价均为每平方米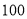 元.若围围墙用了
元.若围围墙用了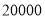 元,问如何围可使竹篱笆用料最省?
元,问如何围可使竹篱笆用料最省? -
科目: 来源: 题型:
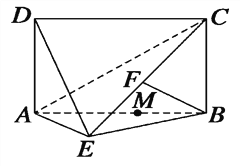
查看答案和解析>>【题目】如图,四边形ABCD为矩形,DA⊥平面ABE,AE=EB=BC=2,
BF⊥平面ACE,且点F在CE上.
(1)求证:AE⊥BE;
(2)求三棱锥D—AEC的体积;
(3)设点M在线段AB上,且满足AM=2MB,试在线段CE上确定一点N,
使得MN∥平面DAE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
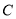 的顶点在原点,焦点在坐标轴上,点
的顶点在原点,焦点在坐标轴上,点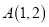 为抛物线
为抛物线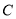 上一点.
上一点.(1)求
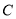 的方程;
的方程;(2)若点
 在
在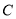 上,过
上,过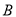 作
作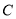 的两弦
的两弦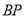 与
与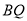 ,若
,若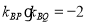 ,求证: 直线
,求证: 直线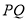 过定点.
过定点. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
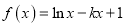 .
.(1)求函数
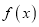 的的单调区间;
的的单调区间;(2)若
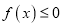 恒成立,试确定实数
恒成立,试确定实数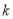 的取值范围;
的取值范围;(3)证明:
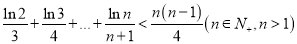 .
.
相关试题

