【题目】已知函数![]() ,
, ![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的图象在
的图象在![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在定义域上为单调增函数.
在定义域上为单调增函数.
①求![]() 最大整数值;
最大整数值;
②证明: ![]() .
.
参考答案:
【答案】(1)![]() (2)①2②见解析
(2)①2②见解析
【解析】试题分析:(1)将![]() 代入到函数
代入到函数![]() ,再对
,再对![]() 求导,分别求出
求导,分别求出![]() 和
和![]() ,即可求出切线方程;(2)①若函数
,即可求出切线方程;(2)①若函数![]() 在定义域上为单调增函数,则
在定义域上为单调增函数,则![]() 恒成立,则先证明
恒成立,则先证明![]() ,构造新函数,求出单调性,再同理可证
,构造新函数,求出单调性,再同理可证![]() ,即可求出
,即可求出![]() 的最大整数值;②由①得
的最大整数值;②由①得![]() ,令
,令![]() ,可得
,可得![]() ,累加后利用等比数列求和公式及放缩法即可得证.
,累加后利用等比数列求和公式及放缩法即可得证.
试题解析:(1)当![]() 时,
时, ![]()
∴![]() ,
,
又![]() ,∴
,∴![]() ,
,
则所求切线方程为![]() ,即
,即![]() .
.
(2)由题意知, ![]() ,
,
若函数![]() 在定义域上为单调增函数,则
在定义域上为单调增函数,则![]() 恒成立.
恒成立.
①先证明![]() .设
.设![]() ,则
,则![]() ,
,
则函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
∴![]() ,即
,即![]() .
.
同理可证![]()
∴![]() ,∴
,∴![]() .
.
当![]() 时,
时, ![]() 恒成立.
恒成立.
当![]() 时,
时, ![]() ,即
,即![]() 不恒成立.
不恒成立.
综上所述, ![]() 的最大整数值为2.
的最大整数值为2.
②由①知, ![]() ,令
,令![]() ,
,
∴![]()
∴![]() .
.
由此可知,当![]() 时,
时, ![]() .当
.当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() ,当
,当![]() 时,
时, ![]() .
.
累加得![]()
![]() .
.
又![]()
 ,
,
∴![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,该几何体是由一个直三棱柱
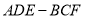 和一个正四棱锥
和一个正四棱锥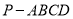 组合而成,
组合而成, 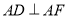 ,
, 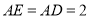 .
.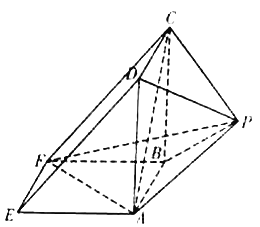
(Ⅰ)证明:平面
 平面
平面 ;
;(Ⅱ)求正四棱锥
 的高
的高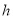 ,使得二面角
,使得二面角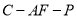 的余弦值是
的余弦值是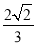 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市政府为了引导居民合理用水,决定全面实施阶梯水价,阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价:若用水量不超过12吨时,按4元/吨计算水费;若用水量超过12吨且不超过14吨时,超过12吨部分按6.60元/吨计算水费;若用水量超过14吨时,超过14吨部分按7.8元/吨计算水费.为了了解全市居民月用水量的分布情况,通过抽样,获得了100户居民的月用水量(单位:吨),将数据按照
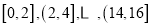 分成8组,制成了如图1所示的频率分布直方图.
分成8组,制成了如图1所示的频率分布直方图.
(Ⅰ)假设用抽到的100户居民月用水量作为样本估计全市的居民用水情况.
(ⅰ)现从全市居民中依次随机抽取5户,求这5户居民恰好3户居民的月用水量都超过12吨的概率;
(ⅱ)试估计全市居民用水价格的期望(精确到0.01);
(Ⅱ)如图2是该市居民李某2016年1~6月份的月用水费
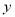 (元)与月份
(元)与月份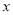 的散点图,其拟合的线性回归方程是
的散点图,其拟合的线性回归方程是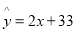 .若李某2016年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.
.若李某2016年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.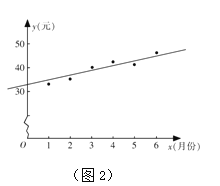
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的四个顶点组成的四边形的面积为
的四个顶点组成的四边形的面积为 ,且经过点
,且经过点 .
.
(1)求椭圆
 的方程;
的方程;(2)若椭圆
 的下顶点为
的下顶点为 ,如图所示,点
,如图所示,点 为直线
为直线 上的一个动点,过椭圆
上的一个动点,过椭圆 的右焦点
的右焦点 的直线
的直线 垂直于
垂直于 ,且与
,且与 交于
交于 两点,与
两点,与 交于点
交于点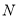 ,四边形
,四边形 和
和 的面积分别为
的面积分别为 .求
.求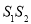 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列
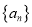 满足
满足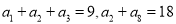 ,数列
,数列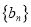 的前
的前 项和为
项和为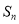 ,且满足
,且满足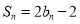 .
.(1)求数列
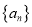 和
和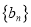 的通项公式;
的通项公式;(2)数列
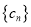 满足
满足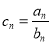 ,求数列
,求数列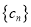 的前
的前 项和
项和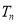 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)求函数
 的单调区间;
的单调区间;(2)若
 恒成立,试确定实数
恒成立,试确定实数 的取值范围;
的取值范围;(3)证明
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知经过
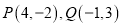 两点的圆
两点的圆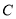 半径小于5,且在
半径小于5,且在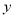 轴上截得的线段长为
轴上截得的线段长为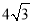 .
.(1)求圆
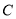 的方程;
的方程;(2)已知直线
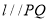 ,若
,若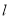 与圆
与圆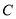 交于
交于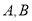 两点,且以线段
两点,且以线段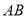 为直径的圆经过坐标原点,求直线
为直径的圆经过坐标原点,求直线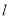 的方程.
的方程.
相关试题

