【题目】![]() ,非空集合
,非空集合![]() ,集合
,集合![]() .
.
(1)![]() 时,求
时,求![]() ;
;
(2)若![]() 是
是![]() 的必要条件,求实数
的必要条件,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)(UB)∩A=[![]() ,
,![]() );(2)
);(2)![]() a
a![]() 或
或![]()
【解析】
(1)先求出集合A、B,再求出UB,借助数轴求出,(UB)∩A.
(2)由题意可知AB,B={x|a<x<a2+2},借助数轴列出AB时区间端点间的大小关系,解不等式组求出a的范围.
(1)对于集合A,(x![]() )(x
)(x![]() )<0,解得,
)<0,解得,![]() x
x![]() ,所以A=(
,所以A=(![]() ,
,![]() ),
),
当a![]() 时,
时,
对于集合B:(x﹣![]() )(x﹣
)(x﹣![]() )<0,解得
)<0,解得![]() <x
<x![]() ,所以B=(
,所以B=(![]() ,
,![]() ),
),
所以UB=(﹣∞,![]() ]∪[
]∪[![]() ,+∞),
,+∞),
所以(UB)∩A=[![]() ,
,![]() );
);
(2)若![]() 是
是![]() 的必要条件,可知AB.
的必要条件,可知AB.
由a2+2>a,得 B={x|a<x<a2+2}.
故![]() ,解得:
,解得:![]() a
a![]() 或
或![]()
综上所述a的取值范围为![]() a
a![]() 或
或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等比数列
 的各项为正数,且
的各项为正数,且 .
.(1)求
 的通项公式;
的通项公式;(2)设
 ,求证数列
,求证数列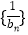 的前
的前 项和
项和 <2.
<2. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的离心率为
的离心率为 ,且过点
,且过点 .
.(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)过椭圆
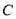 的左焦点的直线
的左焦点的直线 与椭圆
与椭圆 交于
交于 两点,直线
两点,直线 过坐标原点且与直线
过坐标原点且与直线 的斜率互为相反数.若直线
的斜率互为相反数.若直线 与椭圆交于
与椭圆交于 两点且均不与点
两点且均不与点 重合,设直线
重合,设直线 与
与 轴所成的锐角为
轴所成的锐角为 ,直线
,直线 与
与 轴所成的锐角为
轴所成的锐角为 ,判断
,判断 与
与 的大小关系并加以证明.
的大小关系并加以证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
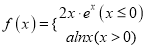 (
( ).
).(1)求
 在
在 上的单调性及极值;
上的单调性及极值;(2)若
 ,对任意的
,对任意的 ,不等式
,不等式 都在
都在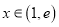 上有解,求实数
上有解,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,a=7,b=8,cosB= –
 .
.(Ⅰ)求∠A;
(Ⅱ)求AC边上的高.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
以平面直角坐标系
 的原点为极点,
的原点为极点,  轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,直线
轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,直线 的参数方程为
的参数方程为 (
( 为参数),圆
为参数),圆 的极坐标方程为
的极坐标方程为 .
. (1)求直线
 的普通方程与圆
的普通方程与圆 的直角坐标方程;
的直角坐标方程; (2)设曲线
 与直线
与直线 交于
交于 两点,若
两点,若 点的直角坐标为
点的直角坐标为 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)证明:
 ;
;(2)证明:对任何正整数n,存在多项式函数
 ,使得
,使得 对所有实数x均成立,其中
对所有实数x均成立,其中 均为整数,当n为奇数时,
均为整数,当n为奇数时, ,当n为偶数时,
,当n为偶数时, ;
;(3)利用(2)的结论判断
 是否为有理数?
是否为有理数?
相关试题

