【题目】选修4-4:坐标系与参数方程
以平面直角坐标系![]() 的原点为极点,
的原点为极点, ![]() 轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,直线
轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),圆
为参数),圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与圆
的普通方程与圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 与直线
与直线![]() 交于
交于![]() 两点,若
两点,若![]() 点的直角坐标为
点的直角坐标为![]() ,求
,求![]() 的值.
的值.
参考答案:
【答案】(1)![]() ,
, ![]() (2)
(2)![]()
【解析】试题分析:(1)根据加减消元法将直线![]() 的参数方程化为普通方程,根据
的参数方程化为普通方程,根据![]() 将圆
将圆![]() 的极坐标方程化为直角坐标方程,(2)先化直线参数方程标准形式,代入圆
的极坐标方程化为直角坐标方程,(2)先化直线参数方程标准形式,代入圆![]() 的直角坐标方程,根据参数几何意义得
的直角坐标方程,根据参数几何意义得![]() ,再根据韦达定理求值.
,再根据韦达定理求值.
试题解析: 解:(1)直线![]() 的普通方程为
的普通方程为![]() ,
,
![]() ,
,
所以![]()
所以曲线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(2)点![]() 在直线
在直线![]() 上,且在圆
上,且在圆![]() 内,由已知直线
内,由已知直线![]() 的参数方程是
的参数方程是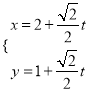 (
(![]() 为参数)
为参数)
代入![]() ,
,
得![]() ,设两个实根为
,设两个实根为![]() ,则
,则![]() ,即
,即![]() 异号
异号
所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
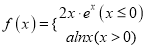 (
( ).
).(1)求
 在
在 上的单调性及极值;
上的单调性及极值;(2)若
 ,对任意的
,对任意的 ,不等式
,不等式 都在
都在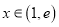 上有解,求实数
上有解,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】
 ,非空集合
,非空集合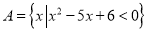 ,集合
,集合 .
.(1)
 时,求
时,求 ;
;(2)若
 是
是 的必要条件,求实数
的必要条件,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,a=7,b=8,cosB= –
 .
.(Ⅰ)求∠A;
(Ⅱ)求AC边上的高.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)证明:
 ;
;(2)证明:对任何正整数n,存在多项式函数
 ,使得
,使得 对所有实数x均成立,其中
对所有实数x均成立,其中 均为整数,当n为奇数时,
均为整数,当n为奇数时, ,当n为偶数时,
,当n为偶数时, ;
;(3)利用(2)的结论判断
 是否为有理数?
是否为有理数? -
科目: 来源: 题型:
查看答案和解析>>【题目】2018年为我国改革开放40周年,某事业单位共有职工600人,其年龄与人数分布表如下:
年龄段




人数(单位:人)
180
180
160
80
约定:此单位45岁~59岁为中年人,其余为青年人,现按照分层抽样抽取30人作为全市庆祝晚会的观众.
(1)抽出的青年观众与中年观众分别为多少人?
(2)若所抽取出的青年观众与中年观众中分别有12人和5人不热衷关心民生大事,其余人热衷关心民生大事.完成下列2×2列联表,并回答能否有90%的把握认为年龄层与热衷关心民生大事有关?

(3)若从热衷关心民生大事的青年观众(其中1人擅长歌舞,3人擅长乐器)中,随机抽取2人上台表演节目,则抽出的2人能胜任才艺表演的概率是多少?

 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在正方体
 中,
中, 是棱
是棱 的中点,
的中点, 是侧面
是侧面 内的动点,且
内的动点,且 平面
平面 ,则
,则 与平面
与平面 所成角的正切值
所成角的正切值 构成的集合是( )
构成的集合是( )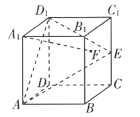
A.
 B.
B.
C.
 D.
D.
相关试题

