【题目】下列说法正确的个数有_________
(1)已知变量![]() 和
和![]() 满足关系
满足关系![]() ,则
,则![]() 与
与![]() 正相关;(2)线性回归直线必过点
正相关;(2)线性回归直线必过点![]() ;
;
(3)对于分类变量![]() 与
与![]() 的随机变量
的随机变量![]() ,
,![]() 越大说明“
越大说明“![]() 与
与![]() 有关系”的可信度越大
有关系”的可信度越大
(4)在刻画回归模型的拟合效果时,残差平方和越小,相关指数![]() 的值越大,说明拟合的效果越好.
的值越大,说明拟合的效果越好.
参考答案:
【答案】3个
【解析】
直接利用线性回归直线的相关理论知识的应用求出结果.
(1)已知变量x和y满足关系y=-2x+3,则x与y正相关;应该是:x与y负相关.故错误.
(2)线性回归直线必过点![]() ,线性回归直线必过中心点.故正确.
,线性回归直线必过中心点.故正确.
(3)对于分类变量A与B的随机变量![]() ,
,![]() 越大说明“A与B有关系”的可信度越大.
越大说明“A与B有关系”的可信度越大.
根据课本上有原句,故正确.
(4)在刻画回归模型的拟合效果时,残差平方和越小,相关指数R2的值越大,说明拟合的效果越好.故正确,根据课本上有原句.
故填3个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂家具车间做A,B型两类桌子,每张桌子需木工和漆工两道工序完成.已知木工做一张A,B型桌子分别需要1小时和2小时,漆工油漆一张A,B型桌子分别需要3小时和1小时;又知木工和漆工每天工作分别不得超过8小时和9小时,设该厂每天做A,B型桌子分别为x张和y张.
(1)试列出x,y满足的关系式,并画出相应的平面区域;
(2)若工厂做一张A,B型桌子分别获得利润为2千元和3千元,那么怎样安排A,B型桌子生产的张数,可使得所得利润最大,最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正项数列
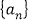 的前
的前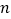 项和为
项和为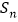 ,且
,且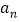 和
和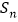 满足:
满足: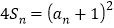
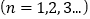 .
.(1)求
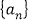 的通项公式;
的通项公式;(2)设
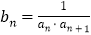 ,求
,求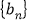 的前
的前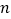 项和
项和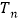 ;
;(3)在(2)的条件下,对任意
 ,
,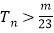 都成立,求整数
都成立,求整数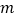 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,多面体
 中,
中, 为正方形,
为正方形, ,二面角
,二面角 的余弦值为
的余弦值为 ,且
,且 .
.(1)证明:平面
 平面
平面 ;
;(2)求平面
 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.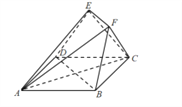
-
科目: 来源: 题型:
查看答案和解析>>【题目】本着健康、低碳的生活理念,租自行车骑游的人越来越多.某自行车租车点的收费标准是每车每次租车时间不超过两小时免费,超过两小时的部分每小时收费标准为2元(不足1小时的部分按1小时计算).有甲、乙两人相互独立来该租车点租车骑游(各租一车一次),设甲、乙不超过两小时还车的概率分别为
 ;两小时以上且不超过三小时还车的概率分别为
;两小时以上且不超过三小时还车的概率分别为 ;两人租车时间都不会超过四小时.
;两人租车时间都不会超过四小时.(1)求出甲、乙两人所付租车费用相同的概率;
(2)求甲、乙两人所付的租车费用之和为4元时的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某项选拔共有四轮考核,每轮设有一个问题,能正确回答问题者进入下一轮考核,否则即被淘汰,.已知某选手能正确回答第一、二、三、四轮的问题的概率分别为
 ,
, ,
, ,
, ,且各轮问题能否正确回答互不影响.
,且各轮问题能否正确回答互不影响.(1)求该选手进入第四轮才被淘汰的概率;
(2)求该选手至多进入第三轮考核的概率;
(3)求该选手回答过四个问题的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个棱长为
 的正方体的表面涂上颜色,将其适当分割成棱长为
的正方体的表面涂上颜色,将其适当分割成棱长为 的小正方体,全部放入不透明的口袋中,搅拌均匀后,从中任取一个,取出的小正方体表面仅有一个面涂有颜色的概率是()
的小正方体,全部放入不透明的口袋中,搅拌均匀后,从中任取一个,取出的小正方体表面仅有一个面涂有颜色的概率是()A.
 B.
B.  C.
C.  D.
D. 
相关试题

